Question

【题目】已知AB是⊙O的直径，AB＝2，点C，点D在⊙O上，CD＝1，直线AD，BC交于点E．

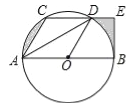
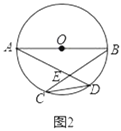
（Ⅰ）如图1，若点E在⊙O外，求∠AEB的度数；

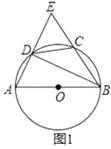
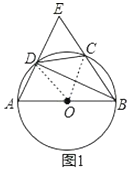
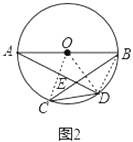
（Ⅱ）如图2，若点E在⊙O内，求∠AEB的度数．

Answer 1

【答案】（Ⅰ）∠AEB＝60°；（Ⅱ）∠AEB＝120°．

【解析】

（Ⅰ）如图1，连接OC、OD，先证明△OCD为等边三角形得到∠COD＝60°，利用圆周角定理得到∠CBD＝30°，∠ADB＝90°，然后利用互余计算出∠AEB的度数；

（Ⅱ）如图2，连接OC、OD，同理可得∠CBD＝30°，∠ADB＝90°，然后根据三角形外角性质计算∠AEB的度数．

解：（Ⅰ）如图1，连接OC、OD，

∵CD＝1，OC＝OD＝1，

∴△OCD为等边三角形，

∴∠COD＝60°，

∴，

∵AB为直径，

∴∠ADB＝90°，

∴∠AEB＝90°﹣∠DBE＝90°﹣30°＝60°；

（Ⅱ）如图2，连接OC、OD，同(Ⅰ)理可得∠CBD＝30°，∠ADB＝90°，

∴∠AEB＝90°+∠DBE＝90°+30°＝120°．