题目内容
【题目】已知：抛物线l，y＝x2+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，﹣3）．
（1）求抛物线l的顶点P的坐标为的A的坐标；
（2）将抛物线l先向上平移3个单位长度，再向左平移2个单位长度，得到抛物线l1，请直接写出平移后的抛物线l1的表达式；
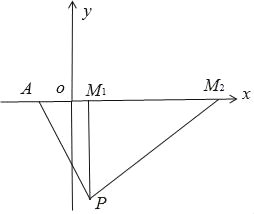
（3）将抛物线l向右平移m个单位长度，得到抛物线l2，其中点A的对应点为点M，若点M、A、P是恰好一个矩形的三个顶点，请求出m的值
【答案】（1）P（1，﹣4），A（﹣1，0）；（2）y＝x2+2x；（3）10
【解析】
（1）待定系数法求出解析式，即可求出P和A点坐标；
（2）抛物线平移按照左加右减的规则得到新解析式；
（3）A、P是已知点，所以以AP为边和对角线两种情况分类讨论即可．
（1）将B、C两点代入得
解得
解析式为y＝x2﹣2x﹣3
∴P（1，﹣4），A（﹣1，0）
（2）抛物线平移后解析式为y＝x2+2x
（3）抛物线平移后解析式为y＝x2﹣2（m+1）x+m2+2m
则点M坐标为（﹣1+m，0）
当M1为直角顶点时，M1（1，0）∴m的值为2
当M2为直角顶点时，
△AM1P∽△M1PM2
∴
＝ 
∴M1M2＝8
∴M2（9，0）
∴m的值为10
练习册系列答案
相关题目
