题目内容
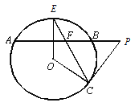
【题目】如图,在△ABC中,AC=BC=4![]() ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
【答案】![]()
【解析】
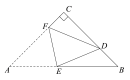
先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF,求出CD=![]() ,CF=x,再根据勾股定理即可求解.
,CF=x,再根据勾股定理即可求解.
解:∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,∠A=∠EDF,
∵△ABC是等腰直角三角形,
∴∠A=∠B=∠EDF=45°,
由三角形外角性质得:∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
∵CD=3DB,![]() ,
,
∴CD=![]() ,
,
设CF=x,则DF=FA=![]() ,
,
∴在Rt△CDF中,由勾股定理得,
CF2+CD2=DF2,
即![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴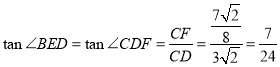 ;
;
故答案为:![]() .
.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目