题目内容
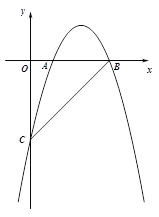
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象交于点
在第一象限内的图象交于点![]() .
.
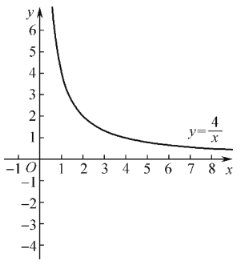
(1)求m、b的值;
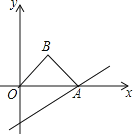
(2)点B在反比例函数的图象上,且点B的横坐标为1.若在直线l上存在一点P(点P不与点A重合),使得![]() ,结合图象直接写出点P的横坐标
,结合图象直接写出点P的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 且
且![]()
【解析】
(1)把![]() 代入到反比例函数关系式中求出m,得到
代入到反比例函数关系式中求出m,得到![]() 点坐标,把
点坐标,把![]() 点坐标代入到
点坐标代入到![]() 中求出b的值即可;
中求出b的值即可;
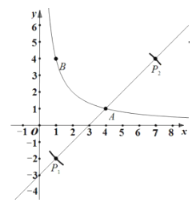
(2)以![]() 为圆心,以
为圆心,以![]() 的长为半径画弧,与l交于点P1,P2,求出P1,P2的横坐标即可,注意:点P不与点A重合.
的长为半径画弧,与l交于点P1,P2,求出P1,P2的横坐标即可,注意:点P不与点A重合.
解:(1)∵![]() 经过点
经过点![]()
∴![]()
∴![]() ,
,
∵![]() 经过点
经过点![]()
∴![]() ,
,![]() ;
;
(2)![]() 且
且![]()
解:∵点B在反比例函数的图象上,且点B的横坐标为1,
∴![]() ,
,
∴点B的坐标为:![]() ,
,
由(1)知:![]() ,
,
∴![]() ,
,
以![]() 为圆心,以
为圆心,以![]() 的长为半径画弧,与l交于点P1,P2,
的长为半径画弧,与l交于点P1,P2,
设![]() ,由题意可知:
,由题意可知:
![]() ,
,
当![]() 时,即
时,即![]()
解得:![]() ,
,
即:![]() 的横坐标为1,
的横坐标为1,![]() 的横坐标为7,
的横坐标为7,
∵满足的是![]() ,
,
∴![]() ,
,
∵点P不与点A重合,
∴![]() ,
,
综上所述:P的横坐标![]() 的取值范围:
的取值范围:![]() 且
且![]() .
.

练习册系列答案
相关题目