Question

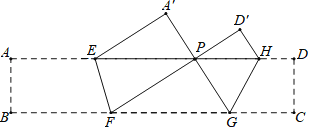
【题目】如图，把某矩形纸片ABCD沿EF，GH折叠（点E，H在AD边上，点F，G在BC边上），使点B和点C落在AD边上同一点P处，A点的对称点为A′点，D点的对称点为D′点，若∠FPG＝90°，△A′EP的面积为8，△D′PH的面积为2，则矩形ABCD的面积等于 （ ）

A.B.C.D.16＋12

Answer 1

【答案】C

【解析】

依据△A′EP∽△D′PH，△A′EP的面积为8，△D′PH的面积为2，即可得出△A′EP与△D′PH的相似比为2：1，设AB=A'P=x，则CD=D'P=x，D'H=x，A'E=x，再根据△D′PH的面积为2，即可得到x=2，进而得出A'E=AE=4，A'P=2=D'P，D'H=DH=，依据勾股定理可得Rt△A'EP中，EP=2，Rt△D'PH中，PH=，最后根据矩形ABCD的面积等于AD×AB进行计算即可．

由折叠可得，∠A'PF=∠B=90°，∠D'PH=∠C=90°，而∠FPG=90°，

∴∠A'PD'=90°，

∴∠A'PE+∠D'PH=∠A'PE+∠A'EP=90°，

∴∠A'EP=∠D'PH，

又∵∠A'=∠D'=90°，

∴△A′EP∽△D′PH，

∵四边形ABC是矩形，

∴AB=CD，AD=BC，设AB=CD=x，

由翻折可知：PA′=AB=x，PD′=CD=x，

∵△A′EP的面积为8，△D′PH的面积为2，

又∵△A′EP∽△D′PH，

∴A′P：D′H=2，∵PA′=x，

∴D′H＝x，

∵xx=2，

∴x=2（负根已经舍弃），

∴AB=CD=2，PE=，PH=，

∴AD=，

∴矩形ABCD的面积=AB×AD=．

故选：C