МвДїДЪИЭ
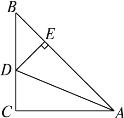
ЎѕМвДїЎїТСЦЄµгCОЄПЯ¶ОABЙПТ»µгЈ¬·Ц±рТФACЎўBCОЄ±ЯФЪПЯ¶ОABН¬ІаЧчЎчACDєНЎчBCE,ЗТCA=CDЈ¬CB=CEЈ¬ЎПACD=ЎПBCE=¦БЈ¬Ц±ПЯAEУлBDЅ»УЪµгF.
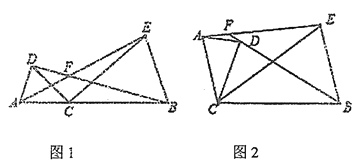
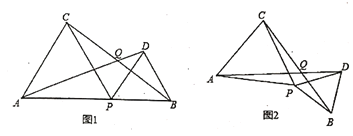
ЈЁ1Ј©ИзНј1ЛщКѕЈ¬
ўЩЗуЦ¤AE= BD
ўЪЗуЎПAFB (УГє¬¦БµДґъКэКЅ±нКѕ)
ЈЁ2Ј©Ѕ«Нј1ЦРµДЎчACDИЖµгCЛіК±ХлРэЧЄДіёцЅЗ¶И(Ѕ»µгFЦБЙЩФЪBDЎўAEЦРµДТ»МхПЯ¶ОЙП)Ј¬µГµЅИзНј2ЛщКѕµДНјРОЈ¬ИфЎПAFB= 150ЎгЈ¬ЗлЦ±ЅУРґіцґЛК±¶ФУ¦µД¦БµДґуРЎ(І»УГЦ¤Гч)
Ўѕґр°ёЎїЈЁ1Ј©ўЩјыЅвОцЈ¬ўЪ180Ўг -¦БЈЁ2Ј©30Ўг
ЎѕЅвОцЎї
ЈЁ1Ј©ўЩУЙЎПACD=ЎПBCE=¦БЈ¬µГµЅЎПACE=ЎПDCB=180Ўг![]() Ј¬И»єуµГµЅЎчACEЎХDCBЈ¬јґїЙµГµЅAE=BDЈ»
Ј¬И»єуµГµЅЎчACEЎХDCBЈ¬јґїЙµГµЅAE=BDЈ»
ўЪУЙўЩЦЄЎчACEЎХDCBЈ¬ФтЎПCAF=ЎПCDFЈ¬АыУГИэЅЗРОДЪЅЗєН¶ЁАнЈ¬УЙЎПCAF+ЎПAFB+ЎПB=180ЎгЈ¬ЎПCDF+ЎПDCB+ЎПB=180ЎгЈ¬ФтЎПAFB=ЎПDCB=![]() Ј»
Ј»
ЈЁ2Ј©УЙЎПAFB= 150ЎгЈ¬ФтЎПEFB=![]() Ј¬УЙЎПACD=ЎПBCEЈ¬µГЎПACE=ЎПDCBЈ¬И»єуµГµЅЎчACEЎХЎчDCBЈ¬µГµЅЎПAEC=ЎПDBCЈ¬ФтЎПBCE=ЎПEFB=30Ўг.
Ј¬УЙЎПACD=ЎПBCEЈ¬µГЎПACE=ЎПDCBЈ¬И»єуµГµЅЎчACEЎХЎчDCBЈ¬µГµЅЎПAEC=ЎПDBCЈ¬ФтЎПBCE=ЎПEFB=30Ўг.
ЅвЈєЈЁ1Ј©ИзНј1Јє
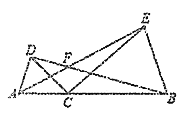
ўЩЦ¤ГчЈєЎЯЎПACD=ЎПBCE=¦БЈ¬
Ўа180Ўг![]() ЎПACD=180Ўг
ЎПACD=180Ўг![]() ЎПBCEЈ¬
ЎПBCEЈ¬
јґЎПACE=ЎПDCB=180Ўг![]() Ј¬
Ј¬
ЎЯCA=CDЈ¬CB=CEЈ¬
ЎаЎчACEЎХDCBЈ¬
ЎаAE=DBЈ»
ўЪЎЯЎчACEЎХDCBЈ¬
ЎаЎПCAF=ЎПCDFЈ¬
УЙИэЅЗРОДЪЅЗєН¶ЁАнЈ¬µГ
ЎПCAF+ЎПAFB+ЎПB=180ЎгЈ¬ЎПCDF+ЎПDCB+ЎПB=180ЎгЈ¬
ЎаЎПAFB=ЎПDCB=![]() Ј»
Ј»
ЈЁ2Ј©ИзНј2Јє
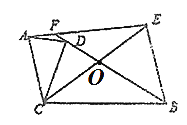
ЎЯЎПAFB= 150ЎгЈ¬
ЎаЎПEFB=![]() Ј¬
Ј¬
ЎЯЎПACD=ЎПBCEЈ¬
ЎаЎПACD+ЎПDCO=ЎПBCE+ЎПDCOЈ¬
ЎаЎПACE=ЎПDCBЈ¬
ЎЯAC=DCЈ¬CE=CBЈ¬
ЎаЎчACEЎХЎчDCBЈ¬
ЎаЎПAEC=ЎПDBCЈ¬
ЎЯЎПFOE=ЎПCOBЈ¬
ЎаЎПBCE=ЎПEFB=30ЎгЈ¬
Ўа![]() .
.

 ЗбЗЙ¶б№ЪЦЬІвФВїјЦ±НЁГыРЈПµБРґр°ё
ЗбЗЙ¶б№ЪЦЬІвФВїјЦ±НЁГыРЈПµБРґр°ё