题目内容
【题目】如图,在△ABC中,AB=AC,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=12,则△DEC的周长为_____.
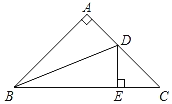
【答案】12
【解析】
首先根据∠A=90°,BD是∠ABC的平分线,DE⊥BC,得出∠A=∠BED,∠ABD=∠EBD,然后判定△ABD≌△EBD(AAS),得出AB=BE,DA=DE,即可得出△DEC的周长.
∵∠A=90°,BD是∠ABC的平分线,DE⊥BC
∴∠A=∠BED,∠ABD=∠EBD
在△ABD和△EBD中,
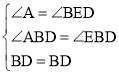 ,
,
∴△ABD≌△EBD(AAS)
∴AB=BE,DA=DE,
∴△DEC的周长=DE+DC+EC=AD+DC+EC=AC+CE=AB+EC=BE+EC=BC=12,
故答案为:12.

练习册系列答案
相关题目
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
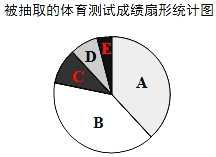
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.