题目内容
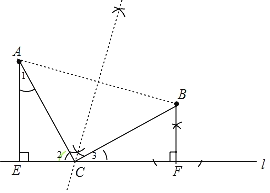
【题目】如图,已知点A、B以及直线l,AE⊥l,垂足为点E.
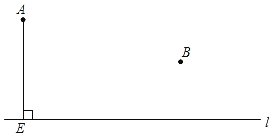
(1)过点B作BF⊥l,垂足为点F;
(2)在直线l上求作一点C,使CA=CB;
(要求:第(1)、(2)小题用尺规作图,并在图中标明相应字母,保留作图痕迹,不写作法.)
(3)在所作的图中,连接CA、CB,若∠ACB=90°,求证:△AEC≌△CFB.
【答案】(1)详见解析;(2)详见解析;(3)详见解析;
【解析】
(1)利用尺规作图法,任取一点,使点在点B的两侧,以B点为圆心,B点到该点的长为半径画弧,交直线于两点,再分别以这两点为圆心,以大于两点一半距离为半径画弧,两弧相交于一点,连接点B与该点与直线l交于点F,即为所求点;
(2)利用尺规作图法,在线段AB的两端点用同一半径画弧,在线段的两旁各得一个交点,将此两交点连接起来,这个连线即为线段的垂直平分线,与直线l交于点C,即为所求点;
(3)首先由AE⊥l,得出∠AEC=90°,∠1+∠2=90°,再由∠ACB=90°,∠3+∠2=90°,得出∠1=∠3,即可判定△AEC≌△CFB.
(1)解:如图,直线BF就是要求作的垂线;
(2)解:如图,点C就是所要求作的点;
(3)证明:∵AE⊥l,
∴∠AEC=90°,∠1+∠2=90°.
∵∠ACB=90°,
∴∠3+∠2=90°.
∴∠1=∠3,
在△AEC和△CFB中
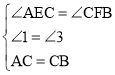
∴△AEC≌△CFB (AAS).

练习册系列答案
相关题目