Question

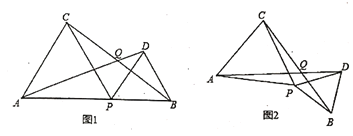
【题目】如图1，点是线段上的动点（点与不重合），分别以为边向线段的同一侧作正和正.

（1）请你判断与有怎样的数量关系？请说明理由；

（2）连接，相交于点，设，那么的大小是否会随点的移动而变化？请说明理由；

（3）如图2，若点固定，将绕点按顺时针方向旋转（旋转角小于），此时的大小是否发生变化？（只需直接写出你的猜想，不必证明）

Answer 1

【答案】（1），见解析；（2）的大小不会随点的移动而变化，见解析；（3）此时的大小不会发生改变，始终等于.

【解析】

（1）先根据SAS证明≌，再根据全等三角形的性质即得结论；

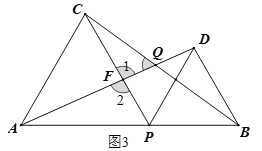
（2）如图3，根据≌ 可得，再在△APF和△CQF中用三角形内角和定理即可证得结论；

（3）旋转的过程中，（2）中的两个三角形的全等关系不变，因而角度不会变化．

解：（1）.

理由如下：

因为是等边三角形，

所以，

又因为是等边三角形，

所以，

又因为三点在同一直线上，

所以.

在和中

所以≌ （SAS）.

所以.

（2）的大小不会随点的移动而变化。

理由如下：如图3，因为≌ ，

所以，

因为，，

又因为，

所以.

（3）因为旋转的过程中，（2）中的两个三角形的全等关系不变，所以角度不会变化．

所以的大小不会发生改变，始终等于.