题目内容
【题目】如图，长方形纸片
中，
，将纸片折叠，使顶点
落在边
上的
点处，折痕的一端
点在边
上.
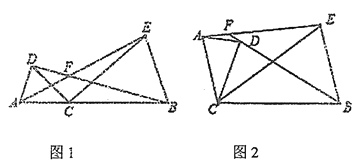
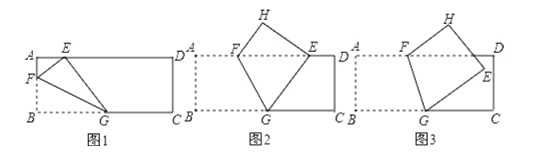
（1）如图1，当折痕的另一端
在
边上且
时，求
的长
（2）如图2，当折痕的另一端在边上且
时，
①求证：
.②求的长.
（3）如图3，当折痕的另一端在边上，点的对应点在长方形内部，到的距离为2
，且时，求的长.
【答案】（1）3；（2）①证明见解析；②6；（3）
.
【解析】
（1）根据翻折的性质可得BF=EF，然后用AF表示出EF，在Rt△AEF中，利用勾股定理列出方程求解即可；
（2）①根据翻折的性质可得∠BGF=∠EGF，再根据两直线平行，内错角相等可得∠BGF=∠EFG，从而得到∠EGF=∠EFG，再根据等角对等边证明即可；
②根据翻折的性质可得EG=BG，HE=AB，FH=AF，然后在Rt△EFH中，利用勾股定理列式计算即可得解；
（3）设EH与AD相交于点K，过点E作MN∥CD分别交AD、BC于M、N，然后求出EM、EN，在Rt△ENG中，利用勾股定理列式求出GN，再根据△GEN和△EKM相似，利用相似三角形对应边成比例列式求出EK、KM，再求出KH，然后根据△FKH和△EKM相似，利用相似三角形对应边成比例列式求解即可．
（1）纸片折叠后顶点
落在边
上的
点处，
∴
，
∵
，
∴
，
在
中，
，
即
，
解得
；
（2）①∵纸片折叠后顶点落在边上的点处，
∴
，
∵长方形纸片
的边
，
∴
，
∴
，
∴
；
②∵纸片折叠后顶点落在边上的点处，
∴
，
，
，
∴
，
在
中，
，
∴
；
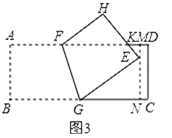
（3）法一：如图3，设
与相交于点
，过点作
分别交、
于
、
，
∵到的距离为2cm，
∴
，
.
在
中，
，
∵
，
，
∴
.
又∵
，
∴
∽
，
∴
，
即
，
解得
，
，
∴
，
∵
，
，
∴
∽
，
∴
，
即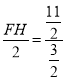
，
解得
，
∴
.
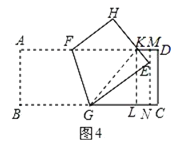
法二：如图4，设与相交于点，过点作分别交、于、，过点作
交于点
，连接
，
∵到的距离为2
，
∴，，
在中，，
设
，
在
中，根据勾股定理可得：
，
在
中，根据勾股定理可得：
，
在
中，根据勾股定理可得：
，
即
，解得：
，故
，
∴，
设
，
在中，根据勾股定理可得：
，
∵
即：
，
解得：
，
∴
