题目内容
在等腰梯形ABCD中，AD∥BC，AB=DC，且BC=2．以CD为直径作⊙O1交AD于点E，过点E作EF⊥AB于点F．建立如图所示的平面直角坐标系，已知A、B两点坐标分别为A（2，0），B（0，2
）．
（1）求C，D两点的坐标；
（2）求证：EF为⊙O1的切线；
（3）线段CD上是否存在点P，使以点P为圆心，PD为半径的⊙P与y轴相切．如果存在，请求出P点坐标；如果不存在，请说明理由．
| 3 |
（1）求C，D两点的坐标；
（2）求证：EF为⊙O1的切线；
（3）线段CD上是否存在点P，使以点P为圆心，PD为半径的⊙P与y轴相切．如果存在，请求出P点坐标；如果不存在，请说明理由．
（1）连CE，如图，
∵CD为⊙O1的直径，
∴CE⊥DE，
∵四边形ABCD是等腰梯形，BC=2，A（2，0），B（0，2
）．
∴DE=OA=2，
∴OD=2+2=4，
∴C点坐标为（-2，2
），D点坐标为（-4，0）；
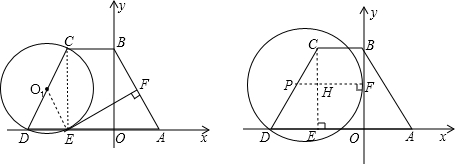
（2）证明：∵DE=2，DC=AB=
=4，
∴∠DCE=30°，
∴∠CDE=∠A=60°，
∴△O1DE为等边三角形，
∴∠O1ED=60°，
而EF⊥AB，
∴∠FEA=30°，
∴∠O1EF=90°，
∴EF为⊙O1的切线；
（3）存在．理由如下：
设⊙P与y轴切与F，连PF，过C作CE⊥x轴与E，交PF于H，⊙P的半径为R，如图，
∴PF⊥y轴，
∴PD=PF=R，
∴PH=R-2，PC=4-R，DE=2，
易证得Rt△CPH∽Rt△CDE，
∴
=
=
，即
=
=
，解得R=
，CH=
，
∴HE=2
-
=
，
∴P点坐标为（-
，
）．
∵CD为⊙O1的直径，
∴CE⊥DE，
∵四边形ABCD是等腰梯形，BC=2，A（2，0），B（0，2
| 3 |
∴DE=OA=2，
∴OD=2+2=4，
∴C点坐标为（-2，2
| 3 |
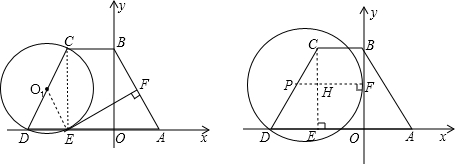
（2）证明：∵DE=2，DC=AB=
(2
|
∴∠DCE=30°，
∴∠CDE=∠A=60°，
∴△O1DE为等边三角形，
∴∠O1ED=60°，
而EF⊥AB，
∴∠FEA=30°，
∴∠O1EF=90°，
∴EF为⊙O1的切线；
（3）存在．理由如下：
设⊙P与y轴切与F，连PF，过C作CE⊥x轴与E，交PF于H，⊙P的半径为R，如图，
∴PF⊥y轴，
∴PD=PF=R，
∴PH=R-2，PC=4-R，DE=2，
易证得Rt△CPH∽Rt△CDE，
∴
| PH |
| DE |
| CP |
| CD |
| CH |
| CE |
| R-2 |
| 2 |
| 4-R |
| 4 |
| CH | ||
2
|
| 8 |
| 3 |
2
| ||
| 3 |
∴HE=2
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
∴P点坐标为（-
| 8 |
| 3 |
4
| ||
| 3 |
练习册系列答案
相关题目
MAN的角平分线于E，过点E作ED⊥AM，垂足为D，反向延长ED交AN于F．