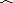题目内容
如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点,
(Ⅰ)求∠AOD的度数;
(Ⅱ)若AO=8cm,DO=6cm,求OE的长.

(Ⅰ)求∠AOD的度数;
(Ⅱ)若AO=8cm,DO=6cm,求OE的长.

(Ⅰ)∵AB∥CD,
∴∠BAD+∠ADC=180°;
∵⊙O内切于梯形ABCD,
∴AO平分∠BAD,有∠DAO=
∠BAD,
DO平分∠ADC,有∠ADO=
∠ADC,
∴∠DAO+∠ADO=
(∠BAD+∠ADC)=90°,
∴∠AOD=180°-(∠DAO+∠ADO)=90°;
(Ⅱ)∵在Rt△AOD中,AO=8cm,DO=6cm,
∴由勾股定理,得AD=
=10cm,
∵E为切点,
∴OE⊥AD,则有∠AEO=90°,
∵S△AOD=
OD•OA=
AD•OE;
∴OE=
=4.8cm.

∴∠BAD+∠ADC=180°;
∵⊙O内切于梯形ABCD,
∴AO平分∠BAD,有∠DAO=
| 1 |
| 2 |
DO平分∠ADC,有∠ADO=
| 1 |
| 2 |
∴∠DAO+∠ADO=
| 1 |
| 2 |
∴∠AOD=180°-(∠DAO+∠ADO)=90°;
(Ⅱ)∵在Rt△AOD中,AO=8cm,DO=6cm,
∴由勾股定理,得AD=
| AO2+DO2 |
∵E为切点,
∴OE⊥AD,则有∠AEO=90°,
∵S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=
| AO•OD |
| AD |


练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

 ,垂足为F.
,垂足为F.