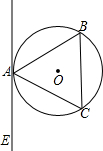
题目内容
如图，AB、AC为⊙O的切线，B、C是切点，延长OB到D，使BD=OB，连接AD，如果∠DAC=78°，那么∠ADO等于（ ）
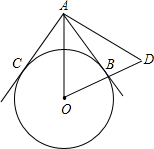
| A．70° | B．64° | C．62° | D．51° |
连接OC．
则OC=OB，AC=AB，OA=OA，△AOC≌△AOB．
∴∠CAO=∠BAO．
∵AB是⊙O的切线，
∴OB⊥AB．
∵BD=OB，
∴AB是线段OD的垂直平分线，OA=AD．
∴∠OAB=∠DAB=∠OAC=
×78°=26°．
∠ADO=180°-∠ABD-∠DAB=180°-90°-26°=64°．
故选B．
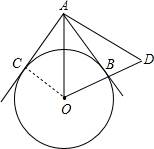
则OC=OB，AC=AB，OA=OA，△AOC≌△AOB．
∴∠CAO=∠BAO．
∵AB是⊙O的切线，
∴OB⊥AB．
∵BD=OB，
∴AB是线段OD的垂直平分线，OA=AD．
∴∠OAB=∠DAB=∠OAC=
| 1 |
| 3 |
∠ADO=180°-∠ABD-∠DAB=180°-90°-26°=64°．
故选B．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
