Question

【题目】如图，AB⊥BC，DC⊥BC，垂足分别为B、C，设AB=4，DC=1，BC=4．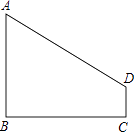

（1）求线段AD的长．
（2）在线段BC上是否存在点P，使△APD是等腰三角形？若存在，求出线段BP的长；若不存在，请说明理由．

Answer 1

【答案】
（1）解：如图1，过D作DE⊥AB于E点，

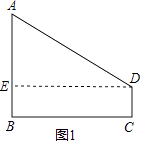
AE=4﹣1=3，DE=BC=4，

在Rt△AED中，AD= =5；

（2）解：如图2，

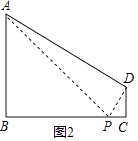
当AP=AD时，

在Rt△ABP中，BP= =3；

如图3，

当PA=PD时，

AB2+BP2=CD2+（BC﹣BP）2，即42+BP2=12+（4﹣BP）2，

解得BP= ．

综上所述，线段BP的长是3或 ．

【解析】（1）根据已知可知四边形ABCD是梯形，要解决梯形的问题通过作高，转化到直角三角形中解决。因此过D作DE⊥AB于E点，可证得BCDE是矩形，就可求出DE和AE的长，再根据勾股定理在Rt△AED中求出AD的长。
（2）根据题意可知，分两种情况，当AP=AD时，在Rt△ABP中，利用勾股定理求出BP的长；当PA=PD时，根据勾股定理，利用PA2=PD2，建立方程，求解即可。
【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念，掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．