题目内容
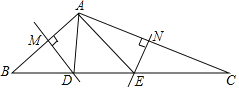
【题目】如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,点E,F分别是边AB,AC的中点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
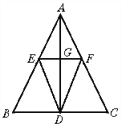
【答案】见解析
【解析】试题(1)首先利用等腰三角形的性质得到∠B=∠C,再结合平行线的性质得到∠AEF=∠AFE,利用等角对等边即可证得;
(2)根据等腰三角形三线合一的性质证得AD是线段EF的垂直平分线,然后根据线段的垂直平分线的性质即可证得.
试题解析:(1)∵EF∥BC,
∴∠AEF=∠B,∠AFE=∠C.
又∵AB=AC,
∴∠B=∠C,
∴∠AEF=∠AFE,
∴AE=AF,即△AEF是等腰三角形;
(2)DE=DF.理由如下:
∵AD是等腰三角形ABC的底边上的高,
∴AD也是∠BAC的平分线,
又∵△AEF是等腰三角形,
∴AG是底边EF上的高和中线,
∴AD⊥EF,GE=GF,
∴AD是线段EF的垂直平分线,
∴DE=DF.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目