题目内容
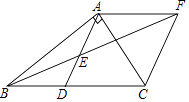
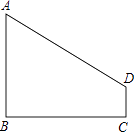
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,CD=1.5,BD=2.5,求AC的长.

【答案】3.
【解析】
过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得CD=DE,再利用勾股定理列式求出BE,然后设AC=AE=x,根据勾股定理列式计算即可得解.
如图,过D作DE⊥AB于E.
∵∠C=90°,AD平分∠CAB,CD=1.5,∴DE=CD=1.5.
在Rt△DEB中,由勾股定理得:BE=![]() =
=![]() =2.
=2.
∵AD=AD,CD=DE,∠C=∠AED,∴Rt△ACD≌Rt△AED,∴AC=AE.
设AC=AE=x,则AB=x+2,由勾股定理得:AB2=AC2+CB2,即(x+2)2=x2+42,解得:x=3,∴AC=3.

练习册系列答案
相关题目