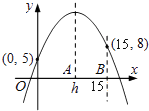题目内容
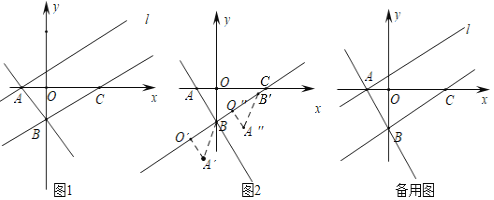
【题目】如图1,在平面直角坐标系中,点![]() 在
在![]() 轴正半轴,点
轴正半轴,点![]() 在
在![]() 轴负半轴,连接
轴负半轴,连接![]() ,
,![]() ,
,![]()
(1)求点![]() 坐标
坐标
(2)如图2,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为直角边做等腰直角
为直角边做等腰直角![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
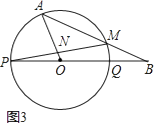
(3)在(2)的条件下,如图3,在![]() 延长线上有一点
延长线上有一点![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.



【答案】(1) 点B坐标为(-2,0),(2) 点E的坐标(2-m,m),(3)F点(1,3).
【解析】
(1)根据△AOB是等腰直角三角形可求出OA、OB长,即可得到B的坐标;
(2)作DM⊥OB,EN⊥X轴,垂足分别为M、N,易证△DOM≌△OEN,从而DM=ON,OM=EN,即可得到E点坐标;
(3)延长OD交HF延长线于P点,在y轴正半轴取R点使OR=OH,过F点作FM垂直于y轴,将AF=![]() GH转化为MF=GH=PR,再利用△RNP≌△FNM,△BOD≌△PFD,得PF=MR=OB=2, 设MF=m,MN=y,FN=2-y,则MA=m,OH=OR=4+m,用勾股定理和相似列方程组解出m即可解答.
GH转化为MF=GH=PR,再利用△RNP≌△FNM,△BOD≌△PFD,得PF=MR=OB=2, 设MF=m,MN=y,FN=2-y,则MA=m,OH=OR=4+m,用勾股定理和相似列方程组解出m即可解答.
解:(1)∵∠ABO=45°,
∴△AOB是等腰直角三角形,
∴2OB2=AB2,
∵AB=2![]()
∴OB=2,
∴点B坐标为(-2,0)
(2)作DM⊥OB,EN⊥X轴,垂足分别为M、N,
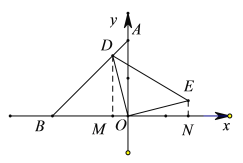
∵∠DOE=90°,
∴∠MDO=∠NOE,
在△DOM和△OEN中
 ,
,
∴△DOM≌△OEN(AAS)
∴DM=ON,OM=EN
∵△BMD、△BOA是等腰直角三角形,EN=OM=-m
∴ON=DM=2+m
∴点E的坐标(2+m,-m),
(3)延长OD交HF延长线于P点,在y轴正半轴取R点使OR=OH,过F点作FM垂直于y轴,
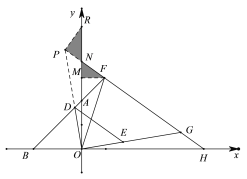
∵△DOE是等腰直角三角形,DE∥FH,
∴△POG是等腰直角三角形,
易证△POR≌△GOH,
∴PR=GH,∠PRN=∠GHO
∵MF⊥y轴,△AOB是等腰直角三角形,
∴△AMF是等腰直角三角形,∠GHO=∠NFM
∴AF=![]() MF,
MF,
又∵AF=![]() GH
GH
∴PR=GH=MF,
在△RNP和△FNM中
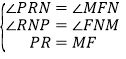 ,
,
△RNP≌△FNM(AAS)
∴PN=MN,FN=RN,
∴PF=MR
在△BOD和△PFD中,
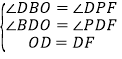
∴△BOD≌△PFD(AAS),
∴PF=OB=MR=2,
设MF=m,MN=y,FN=2-y,则MA=m,OH=OR=4+m
在Rt△MNF中,![]() ,
,
∴![]() ,
,
∵△MFN∽△OHN
∴![]() ,
,
∴![]() ,
,
联立解方程得m=1,
∴F点坐标为(1,3)