题目内容
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),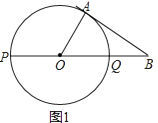
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);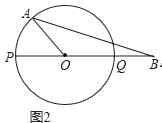
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).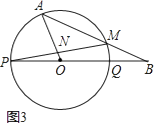
【答案】
(1)解:∵直线AB与圆O相切,
∴∠OAB=90°,
∵OQ=QB=1,
∴OA=1,OB=2,
∴OA= ![]() OB,
OB,
∴∠B=30°,
∴∠AOB=60°,
∴AQ= ![]() ;
;
(2)解:如图1, 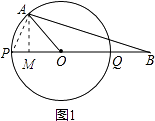
连接AP,过点A作AM⊥BP于M,
∵∠AOB=120°,
∴∠AOP=60°,
∵sin∠AOP= ![]() ,
,
∴AM=sin∠AOPAO=sin60°×1= ![]() ,
,
∵OM= ![]() ,
,
∴BM=OM+OB= ![]() +2=
+2= ![]() ,
,
∴AB= ![]() ;
;
(3)解:如图2,连接MQ,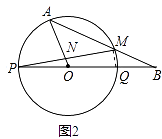
∵PQ为圆O的直径,
∴∠PMQ=90°,
∵ON⊥PM,
∴AO∥MQ,
∵PO=OQ,
∴ON= ![]() MQ,
MQ,
∵OQ=BQ,
∴MQ= ![]() AO,
AO,
∴ON= ![]() AO,
AO,
设ON=x,则AO=4x,
∵OA=1,
∴4x=1,
∴x= ![]() ,
,
∴ON= ![]() ,
,
∴PN= ![]() ,
,
∴tan∠MPQ= 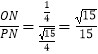 .
.
【解析】(1)先根据直角三角形的性质求出∠B的度数,得到∠AOB的度数,再根据弧长的计算公式进行求解即可。
(2)连接AP,过点A作AM⊥BP于M,根据特殊角的三角函数值和已知条件求出AM,再根据BM=OM+OB,求出BM,最后根据勾股定理求出AB。
(3)连接MQ,先根据PQ是圆O的直径和AO⊥PM,得出ON∥MQ,求出ON与OA的数量关系,设ON=x,则AO=4x,根据OA的值求出x的值,再根据勾股定理求出PN的长,最后根据三角函数的定义即可得出答案。
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.

【题目】雾霾天气严重影响市民的生活质量.在去年寒假期间,某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民.并对调查结果进行了整理.绘制了如图不完整的统计图表.观察分析并回答下列问题.
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) | n |
(1)本次被调查的市民共有多少人?
(2)求m、n的值,并计算图2中区域B所对应的扇形圆心角的度数;
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?
【题目】二次函数 ![]() (a,b,c为常数,且
(a,b,c为常数,且 ![]() )中的
)中的 ![]() 与
与 ![]() 的部分对应值如表:
的部分对应值如表:
| … | -1 | 0 | 1 | 3 | … |
| … | -1 | 3 | 5 | 3 | … |
下列结论:
① ![]() ;
;
②当 ![]() 时,y的值随x值的增大而减小;
时,y的值随x值的增大而减小;
③3是方程 ![]() 的一个根;
的一个根;
④当 ![]() 时,
时, ![]() .
.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个






