题目内容
【题目】如图1,在平面直角坐标系中,直线y=-![]() x-
x-![]() 与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.
与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.
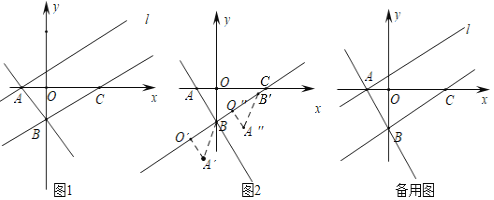
(1)求直线BC的解析式;
(2)作点A关于BC的对称点D,一动点P从C点出发按某一路径运动到直线l上的点M,再沿垂直BC的方向运动到直线BC上的点N,再沿某一路径运动到D点,求点P运动的最短路径的长以及此时点N的坐标;
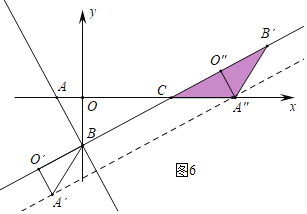
(3)如图2,将△AOB绕点B旋转,使得A′O′⊥BC,得到△A′O′B,将△A′O′B沿直线BC平移得到△A″O″B′,连接A″、B″、C,是否存在点A″,使得△A″B′C为等腰三角形?若存在,请直接写出点A″的坐标;若不存在,请说明理由.
【答案】(1) y=![]() x-
x-![]() ;(2) 2
;(2) 2![]() , N(
, N(![]() ,-
,-![]() );(3)见解析.
);(3)见解析.
【解析】
(1)利用待定系数法即可解决问题;
(2)如图2中,作点C关于直线AF的对称点C′,连接CC′交AF于点F,连接DF交BC于N,作NE⊥AF于E,连接EC,则此时CE+EN+DN的值最小,最小值=线段DF的长;
(3)分四种情形分别画出图形求解即可.
(1)∵直线y=-![]() x-
x-![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,
∴A(-1,0),B(0,-![]() ),
),
∵OC=3OA,
∴OC=3,
∴C(3,0),
设直线BC的解析式为y=kx+b,则有![]() ,
,
解得 ,
,
∴直线BC的解析式为y=![]() x-
x-![]() ;
;
(2)如图2中,作点C关于直线AF的对称点C′,连接CC′交AF于点F,连接DF交BC于N,作NE⊥AF于E,连接EC,则此时CE+EN+DN的值最小,最小值=线段DF的长.

由题意D(1,-2![]() ),
),
∵直线CF的解析式为y=![]() x+
x+![]() ,直线CF的解析式为y=-
,直线CF的解析式为y=-![]() x+3
x+3![]() ,
,
由 ,解得
,解得![]() ,
,
∴F(2,![]() ),
),
∴DF=![]() =2
=2![]() ,
,
∴点P的路径的最小值为2![]() ,
,
∵直线DF的解析式为y=3![]() x-5
x-5![]() ,
,
由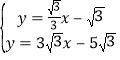 ,解得
,解得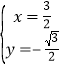 ,
,
∴N(![]() ,-
,-![]() );
);
(3)由题意,BO′=BO=![]() ,AB=BA′=2,OA=O′A′=1,点O′向下平移
,AB=BA′=2,OA=O′A′=1,点O′向下平移![]() 个单位,向右平移
个单位,向右平移![]() 单位得到A′,
单位得到A′,
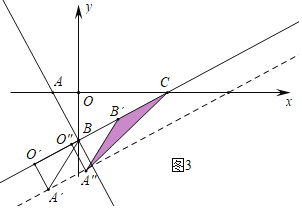
①如图3中,当CB′=B′A″=2时,此时O″(![]() ,-
,-![]() ),可得A″(2-
),可得A″(2-![]() ,-1-
,-1-![]() ).
).
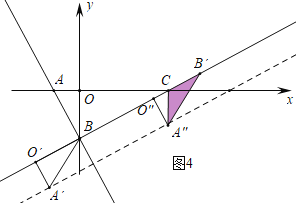
②如图4中,当CB′=CA″时,设CB′=CA″=x,则有x2=12+(![]() -x)2,
-x)2,
可得x=![]() ,此时O″(
,此时O″(![]() ,-
,-![]() ),可得A″(3,-
),可得A″(3,-![]() ).
).
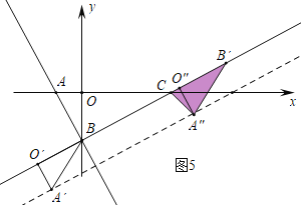
③当B′C=B′A″=2时,O″(![]() ,
,![]() ),可得A″(2+
),可得A″(2+![]() ,1-
,1-![]() )
)
④当CA″=B′A″=2时,O″(![]() ,
,![]() ),可得A″(5,0).
),可得A″(5,0).
综上所述,满足条件的点A″的坐标为(2-![]() ,-1-
,-1-![]() )或(3,-
)或(3,-![]() )或(2+
)或(2+![]() ,1-
,1-![]() )或(5,0).
)或(5,0).

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案