Question

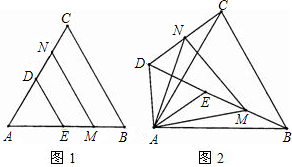
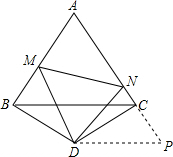
如图所示，等边△ABC的边长为2，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°的角，角的两边分别交AB于M，交AC于N，连接MN，形成一个△AMN，则△AMN的周长为______．

Answer 1

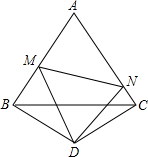
令CP=BM，交AC延长线于P，连接DP．
∵△BDC是等腰三角形，且∠BDC=120°
∴BD=CD，∠DBC=∠DCB=30°
又∵△ABC等边三角形
∴∠ABC=∠ACB=60°
∴∠MBD=∠ABC+∠DBC=90°
同理可得∠NCD=90°
∴∠PCD=∠NCD=∠MBD=90°
又∵CP=BM，
∴△BDM≌△CDP
∴MD=PD
∠MDB=∠PDC
∵∠MDN=60°
∴∠MDB+∠NDC=∠PDC+∠NDC=∠BDC-∠MDN=60°即∠MDN=∠PDN=60°
∴△NMD≌△NPD（SAS）
∴MN=PN=NC+CP=NC+BM
∴△AMN的周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=2+2=4
故△AMN的周长为4．
故填4．