Question

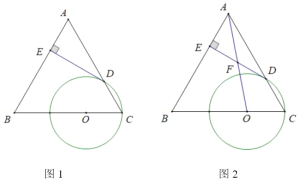
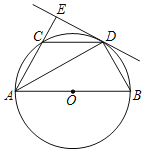
【题目】如图，AB是⊙O的直径，C点在⊙O上，AD平分∠BAC交⊙O于D，过D作直线AC的垂线，交AC的延长线于E，连接BD，CD．

（1）求证：直线DE是⊙O的切线；

（2）若直径AB＝6，填空：

①当AD＝　 　时，四边形ACDO是菱形；

②过D作DH⊥AB，垂足为H，当AD＝　 　时，四边形AHDE是正方形．

Answer 1

【答案】（1）证明见解析；（2）①3②3

【解析】

（1）连接，根据平分，和，可证明，再根据即可证明直线是的切线；

（2）①根据四边形是菱形，可得，得，进而可求的长；

②当，即与重合时，四边形是正方形，根据勾股定理即可得的长．

（1）证明：如图，连接OD，

∵OA＝OD，

∴∠OAD＝∠ODA，

∵AD平分∠BAC，

∴∠CAD＝∠OAD，

∴∠CAD＝∠ODA，

∴AC∥OD，

∵DE⊥AE，

∴∠AED＝90°，

∴∠ODE＝90°，

∴DE⊥OD，OD是⊙O的半径，

∴直线DE是⊙O的切线；

（2）解： ①当时，四边形是菱形，

理由：四边形ACDO是菱形时，OD＝CD＝BD＝OB，

∴∠DBA＝60°，

∵AB是⊙O的直径，

∴∠ADB＝90°，

．

当时，四边形是菱形．

故答案为：；

②过D作DH⊥AB，垂足为H，当时，四边形是正方形．

理由：当DH⊥AB，即DH与DO重合时，四边形AHDE是正方形，

由勾股定理，得．

当时，四边形是正方形．

故答案为：．