题目内容
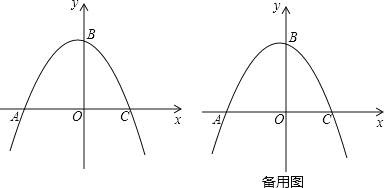
【题目】如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)如图①,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO.求点P的坐标;
(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)抛物线的函数表达式为y=x2+2x﹣3;(2)点P的坐标为![]() ,
,![]() 或
或![]() ,
,![]() ;(3)为定值8.
;(3)为定值8.
【解析】
(1)把点![]() 、
、![]() 坐标代入抛物线解析式即求得
坐标代入抛物线解析式即求得![]() 、
、![]() 的值.
的值.
(2)点![]() 可以在
可以在![]() 轴上方或下方,需分类讨论.①若点
轴上方或下方,需分类讨论.①若点![]() 在
在![]() 轴下方,延长
轴下方,延长![]() 到
到![]() ,使
,使![]() 构造等腰
构造等腰![]() ,作
,作![]() 中点
中点![]() ,即有
,即有![]() ,利用
,利用![]() 的三角函数值,求
的三角函数值,求![]() 、
、![]() 的长,进而求得
的长,进而求得![]() 的坐标,求得直线
的坐标,求得直线![]() 的解析式后与抛物线解析式联立,即求出点
的解析式后与抛物线解析式联立,即求出点![]() 坐标.②若点
坐标.②若点![]() 在
在![]() 轴上方,根据对称性,
轴上方,根据对称性,![]() 一定经过点
一定经过点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,求得直线
,求得直线![]() 的解析式后与抛物线解析式联立,即求出点
的解析式后与抛物线解析式联立,即求出点![]() 坐标.
坐标.
(3)设点![]() 横坐标为
横坐标为![]() ,用
,用![]() 表示直线
表示直线![]() 、
、![]() 的解析式,把
的解析式,把![]() 分别代入即求得点
分别代入即求得点![]() 、
、![]() 的纵坐标,再求
的纵坐标,再求![]() 、
、![]() 的长,即得到
的长,即得到![]() 为定值.
为定值.
解:(1)∵抛物线y=x2+bx+c经过点A(1,0),C(0,﹣3)
![]()
![]() 解得:
解得:![]()
∴抛物线的函数表达式为y=x2+2x﹣3
(2)①若点P在x轴下方,如图1,
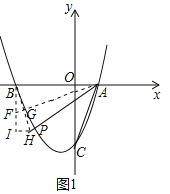
延长AP到H,使AH=AB,过点B作BI⊥x轴,连接BH,作BH中点G,连接并延长AG交BI于点F,过点H作HI⊥BI于点I
∵当x2+2x﹣3=0,解得:x1=﹣3,x2=1
∴B(﹣3,)
∵A(1,0),C(0,﹣3)
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 中,
中,![]() ,
,![]()
∵AB=AH,G为BH中点
∴AG⊥BH,BG=GH
∴∠BAG=∠HAG,即∠PAB=2∠BAG
∵∠PAB=2∠ACO
∴∠BAG=∠ACO
![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,即
,即![]() ,
,![]()
设直线![]() 解析式为
解析式为![]()
![]()
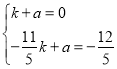 解得:
解得: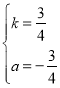
![]() 直线
直线![]()
![]()
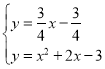 解得:
解得: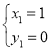 (即点
(即点![]() ,
,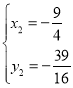
![]() ,
,![]() ;
;
②若点![]() 在
在![]() 轴上方,如图2,
轴上方,如图2,
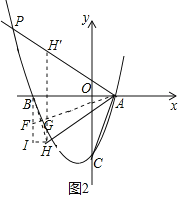
在![]() 上截取
上截取![]() ,则
,则![]() 与
与![]() 关于
关于![]() 轴对称
轴对称
![]() ,
,![]()
设直线![]() 解析式为
解析式为![]()
![]()
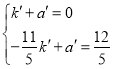 解得:
解得:
![]() 直线
直线![]()
![]()
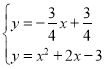 解得:
解得: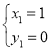 (即点
(即点![]() ,
,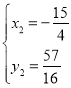
![]() ,
,![]() .
.
综上所述,点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.
(3)![]() 为定值,
为定值,
![]() 抛物线
抛物线![]() 的对称轴为:直线
的对称轴为:直线![]()
![]() ,
,![]()
设![]() ,
,![]()
设直线![]() 解析式为
解析式为![]()
![]()
![]() 解得:
解得: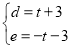
![]() 直线
直线![]()
当![]() 时,
时,![]()
![]()
设直线![]() 解析式为
解析式为![]()
![]()
![]() 解得:
解得:![]()
![]() 直线
直线![]()
当![]() 时,
时,![]()
![]()
![]() ,为定值.
,为定值.