Question

【题目】如图1，菱形ABCD中，∠A=60°，点P从A出发，以2cm/s的速度沿边AB、BC、CD匀速运动到D终止，点Q从A与P同时出发，沿边AD匀速运动到D终止，设点P运动的时间为t（s）．△APQ的面积S（cm2）与t（s）之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出．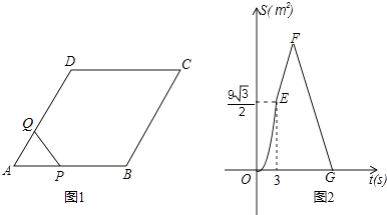

（1）求点Q运动的速度；
（2）求图2中线段FG的函数关系式；
（3）问：是否存在这样的t，使PQ将菱形ABCD的面积恰好分成1：5的两部分？若存在，求出这样的t的值；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由题意，可知题图2中点E表示点P运动至点B时的情形，所用时间为3s，则菱形的边长AB=2×3=6cm．

此时如答图1所示：

AQ边上的高h=ABsin60°=6× = cm，

S=S△APQ= AQh= AQ× = ，解得AQ=3cm，

∴点Q的运动速度为：3÷3=1cm/s

（2）

解：由题意，可知题图2中FG段表示点P在线段CD上运动时的情形．如答图2所示：

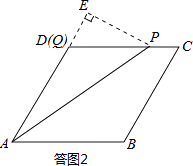
点Q运动至点D所需时间为：6÷1=6s，点P运动至点C所需时间为12÷2=6s，至终点D所需时间为18÷2=9s．

因此在FG段内，点Q运动至点D停止运动，点P在线段CD上继续运动，且时间t的取值范围为：6≤t≤9．

过点P作PE⊥AD交AD的延长线于点E，则PE=PDsin60°=（18﹣2t）× = t+ ．

S=S△APQ= ADPE= ×6×（ t+ ）= t+ ，

∴FG段的函数表达式为：S= t+ （6≤t≤9）

（3）

解：菱形ABCD的面积为：6×6×sin60°= ．

当点P在AB上运动时，PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分，如答图3所示．

此时△APQ的面积S= AQAPsin60°= t2t× = t2，

根据题意，得 t2= × ，

解得t= s（舍去负值）；

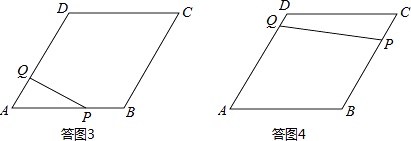
当点P在BC上运动时，PQ将菱形分为梯形ABPQ和梯形PCDQ两部分，如答图4所示．

此时，有S梯形ABPQ= S菱形ABCD，即 （2t﹣6+t）×6× = × ，

解得t= s．

∴存在t= 和t= ，使PQ将菱形ABCD的面积恰好分成1：5的两部分

【解析】（1）根据函数图象中E点所代表的实际意义求解．E点表示点P运动到与点B重合时的情形，运动时间为3s，可得AB=6cm；再由S△APQ= ，可求得AQ的长度，进而得到点Q的运动速度；（2）函数图象中线段FG，表示点Q运动至终点D之后停止运动，而点P在线段CD上继续运动的情形．如答图2所示，求出S的表达式，并确定t的取值范围；（3）当点P在AB上运动时，PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分，如答图3所示，求出t的值；当点P在BC上运动时，PQ将菱形分为梯形ABPQ和梯形PCDQ两部分，如答图4所示，求出t的值．
【考点精析】本题主要考查了二次函数的性质和菱形的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能正确解答此题．