题目内容
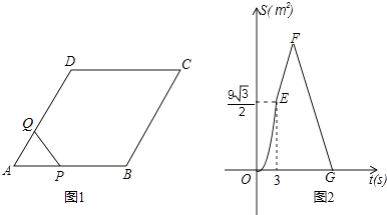
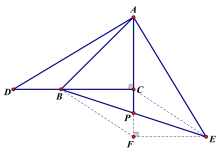
【题目】如图,在等腰△ABC中,∠ACB = 90,点D为CB延长线上一点,过A作AE⊥AD,且AE = AD,BE与AC的延长线交于点P,求证:PB = PE.

【答案】证明见解析.
【解析】
作EM⊥AP于M,证△BCP≌△EMP,求出BC=AC=EM,证△ADC≌△EAM,推出即可;
法1:过E作EF⊥AC,垂足为F,连接BF,CE
∵ AE⊥AD,ACB = 90
∴ EAF + CAD = 90,D + CAD = 90
∴ EAF = D
又∵ AFE = ACB = 90,AE = AD
∴ △AFE ≌△DCA(AAS)
∴ EF=AC=BC
∵ BC⊥AC,EF⊥AC
∴ EF∥BC
∴ EF![]() BC
BC
∴ 四边形BCEF为平行四边形
∴ PB = PE.
法2:∵ AD = AE且AD⊥AE
∴ 可将△ADB绕点A逆时针旋转90至△AEH,
由旋转性质得AH = AB且AH⊥AB
∴ △BAH为等腰直角三角形,ABH = 45
又∵ △ACB中,ACB = 90,AC = BC
∴ ABC = 45
∴ ABH = ABC,则B、C、H三点共线
∴ AP垂直平分BH
∴ PH = PB
∴ PBH = PHB
又由旋转性质得EH⊥BD,即EH⊥BH
∴ PHE = 90-PHB,PEH = 90-PBH,
∴ PEH = PHB
∴ PH=PE
∴ PB=PE

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
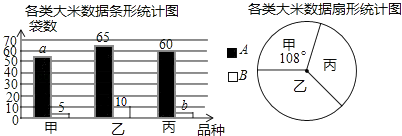
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
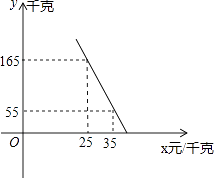
【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是x的函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 当交电费20.5元时,用电量为37千瓦时
D. 若用电量为8千瓦时,则应交电费4.4元