题目内容
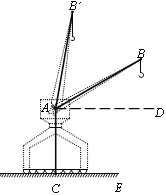
【题目】如图,形如量角器的半圆O的直径DE-12cm,形如三角板的△ABC中,∠ACB=90°,tan∠ABC= ![]() ,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.

(1)点C到直线AB的距离为 ________cm;
(2)当t= ________(s)时,⊙O与AC所在直线第一次相切;当t=________(s)时,⊙O与AC所在直线第二次相切;
(3)当t为何值时,直线AB与半圆O所在的圆相切;
(4)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,直接写出重叠部分的面积。
【答案】(1)6;(2)1,7;(3)t为4秒或16秒;(4)6π+9![]() cm2
cm2
【解析】
(1)由tan∠ABC=![]() , 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=
, 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=![]() AC=6;
AC=6;
(2)由题意可知,DE为⊙O的直径,即OE=6,OC=8,所以EC=2,⊙O与AC所在的直线第一次相切,即点C与点E重合,也就是t=1时;DC=DE+EC=14,⊙O与AC所在的直线第二次相切,即点D与点E重合时,也就是t=7;
(3)此题有两种情况:第一种情况,直线AB与半圆O相切,即过点O的半径与AB所在的直线垂直,也就是CF⊥AB,即点O与点C重合时,也就是t=4;第二种情况,直线Ab与半圆O相切,即点O运动到点B的右侧时,即过点O的半径与AB的延长线垂直,此时OC=24,也就是t=(24+8)÷2=16;
(4)此题有三种情况:第一种情况是⊙O与AC第一次相切时,此时⊙O与△ABC没有重叠部分;第二种情况是O与AB相切时,此时重叠的部分为O的四分之一,即为9πcm2;第三种情况是O与AC第二次相切时,此时⊙O的直径DE与△ABC的边BC重合,重叠部分的面积等于△BOG与扇形GOC的和,即6π+9![]() cm2
cm2
(1)由tan∠ABC=![]() , 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=
, 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=![]() AC=6;
AC=6;
(2)由题意可知,DE为⊙O的直径,即OE=6,OC=8,所以EC=2,⊙O与AC所在的直线第一次相切,即点C与点E重合,也就是t=1时;DC=DE+EC=14,⊙O与AC所在的直线第二次相切,即点D与点E重合时,也就是t=7;
(3)解:如图2,过C作CF⊥AB于F , 同理得:OF=6,
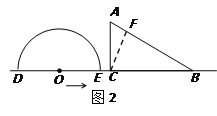
当直线AB与半圆O所在的圆相切时,又∵圆心O到AB的距离为6,半圆的半径为6,
且圆心O又在直线BC上,∴O与C重合,即当O点运动到C点时,半圆O与△ABC的边AB相切,
此时,点O运动了8cm , 所求运动时间t=8÷2=4;
如图3,当点O运动到B点的右侧时,且OB=12,过O作OQ⊥AB , 交直线AB于Q ,

在Rt△QOB中,∠OBQ=30°,则OQ= ![]() OB=6,即OQ与半圆O所在的圆相切,此时点O运动了12+12+8=32cm , 所求运动时间t=32÷2=16,
OB=6,即OQ与半圆O所在的圆相切,此时点O运动了12+12+8=32cm , 所求运动时间t=32÷2=16,
综上所述,当t为4秒或16秒时,直线AB与半圆O所在的圆相切
(4)解:重叠部分的面积为/span>9πcm2或(6π+9 ![]() )cm2 . 有两种情况:
)cm2 . 有两种情况:
①当半圆O与AB边相切于F时,如图1,重叠部分的面积S= ![]() π×62=9π;
π×62=9π;
②当半圆O与AC相切于C时,如图4,连接OG ,
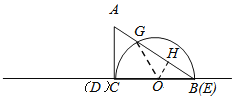
∵BC=DE=12,∴C与D重合,E与B重合,∵OG=OB , ∴∠ABC=∠OGB=30°,
∴∠COG=60°.过O作OH⊥AB于H , ∵OB=6,∴OH= ![]() OB=3,
OB=3,
由勾股定理得:BH=3 ![]() ,∴BG=2BH=6
,∴BG=2BH=6 ![]() ,此时重叠部分的面积S=
,此时重叠部分的面积S= ![]() +
+ ![]() ×6
×6 ![]() ×3=6π+9
×3=6π+9 ![]() ;
;
综上所述,重叠部分的面积为9πcm2或(6π+9 ![]() )cm2
)cm2
圆的综合题
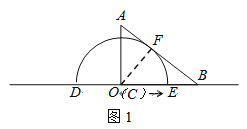
解:(1)如图1,过C作CF⊥AB于F ,
Rt△BCF中,∵tan∠ABC= ![]() ∴∠ABC=30°,BC=12,
∴∠ABC=30°,BC=12,
∴CF= ![]() BC=6,故答案为:6
BC=6,故答案为:6
 ;
;
(2)∵DE=12,∴OE=OD=6,∵OC=8,∴EC=8-6=2,∴t=2÷2=1,
∴当t=1s时,⊙O与AC所在直线第一次相切;∴DC=8+6=14,∴t=14÷2=7,
∴当t=7s时,⊙O与AC所在直线第二次相切;故答案为:1,7