题目内容
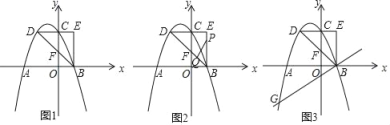
【题目】如图，二次函数
的图像与坐标轴交于点A（1， 0）和点C．经过点A的直线
与二次函数图像交于另一点B，点B与点C关于二次函数图像的对称轴对称．
（1）求一次函数表达式；
（2）点P在二次函数图像的对称轴上，当△ACP的周长最小时，请求出点P的坐标．
【答案】（1）y=x-1；（2）P的坐标（2，1）
【解析】
（1）先利用对称轴方程确定抛物线的对称轴是直线x=2，再利用抛物线的对称性确定点B的坐标（4，3），然后利用待定系数法求一次函数表达式；
（2）连接AB交直线x=2于点P，如图，利用两点之间线段最短判断此时△ACP的周长最小，然后计算自变量为2对应的一次函数值即可得到满足条件的P的坐标．
（1）二次函数y=ax2-4ax+3的对称轴是直线x=-
=2，
而点C的坐标为（0，3），
∵点B与点C关于二次函数图象的对称轴对称．
∴点B的坐标（4，3），
把A（1，0）和B（4，3）代入y=kx+b得
，解得
，
∴一次函数表达式为y=x-1；
（2）连接AB交直线x=2于点P，如图，
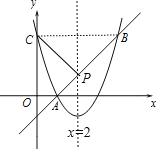
∵点B与点C关于二次函数图象的对称轴对称．
∴PC=PB，
∴PC+PA=PB+PA=AB，
∴此时PC+PA的值最小，△ACP的周长最小，
当x=2时，y=x-1=2-1=1，
∴满足条件的P的坐标（2，1）．
【题目】A城有肥料200吨，B城有肥料300吨．现要把这些肥料全部运往C，D两乡，从A城往C，D两乡运肥料的费用分别为20元/吨和25元/吨；从B城往C，D两乡运肥料的费用分别为15元/吨和24元/吨．现C乡需要肥料240吨，D乡需要肥料260吨．设从A城调往C乡肥料x吨.
(1)根据题意，填写下表：
调入地 数量/吨 调出地 | C | D |
A | x | ______ |
B | _____ | ______ |
总计 | 240 | 260 |
(2)给出完成此项调运任务最节省费用的调运方案及所需费用，并说明理由．
