��Ŀ����
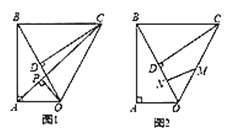
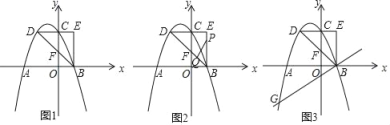
����Ŀ�� ��ͼ1����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y��ax2+bx+5��x�ύ��A����B����y�ύ�ڵ�C������C��CD��y�ύ�������ڵ�D������B��BE��x�ᣬ��DC�ӳ����ڵ�E������BD����y���ڵ�F��ֱ��BD�Ľ���ʽΪy����x+2��
��1��д����E�����ꣻ�����ߵĽ���ʽ��
��2����ͼ2����P���߶�EB�ϴӵ�E���B��1����λ����/����ٶ��˶���ͬʱ����Q���߶�BD�ϴӵ�B���D��![]() ����λ����/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ����PQBΪֱ�������Σ�
����λ����/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ����PQBΪֱ�������Σ�
��3����ͼ3������B��ֱ��BG���������ڵ�G����tan��ABG��![]() ����MΪֱ��BG�Ϸ���������һ�㣬����M��MH��BG������ΪH����HF��MF����ֱ��д�����������ĵ�M�����꣮
����MΪֱ��BG�Ϸ���������һ�㣬����M��MH��BG������ΪH����HF��MF����ֱ��д�����������ĵ�M�����꣮
���𰸡���1����E����Ϊ��2��5����y����![]() x2��
x2��![]() +5����2��t��
+5����2��t��![]() ��
��![]() ʱ����PQBΪֱ�������Σ���3����M����Ϊ����4��3����0��5����
ʱ����PQBΪֱ�������Σ���3����M����Ϊ����4��3����0��5����
��������
��1���ɴ���ϵ����������꼰������ϵʽ��
��2���������⣬��DEBΪ����ֱ�������Σ�ͨ���������ۡ�PQB=90�����QPB=90������������������tֵ��
��3���ӳ�MF��GB��K���ɡ�MHK=90����HF=MF���Ƶ�HF=FK����FΪMK�е㣬���M���꣬�����е��������ʣ���ʾK�����꣬����GB����ʽ������õ�M���꣮
����D��-3��5����B��2��0������y=ax2+bx+5
![]()
���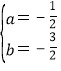
�������߽���ʽΪ��y=-![]() x2-
x2-![]() x+5
x+5
��2������֪��QBE=45����PE=t��PB=5-t��QB=![]() t
t
����QPB=90��ʱ����PQBΪֱ�������Σ�
�ߡ�QBE=45��
��QB=![]() PB
PB
��![]() t��
t��![]() (5t)
(5t)
���t=![]()
����PQB=90��ʱ����PQBΪֱ�������Σ�
��BPQ�ס�BDE
��BQBD=BPBE
��5��5-t��=![]() t5
t5![]()
��ã�t=![]()
��t=![]() ��
��![]() ʱ����PQBΪֱ�������Σ�
ʱ����PQBΪֱ�������Σ�
��3������֪tan��ABG=![]() ����ֱ��GB��B��
����ֱ��GB��B��
��ֱ��GB����ʽΪ��y=![]() x1
x1
�ӳ�MF��ֱ��BG�ڵ�K
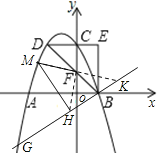
��HF=MF
���FMH=��FHM
��MH��BGʱ
���FMH+��MKH=90��
��FHK+��FHM=90��
���FKH=��FHK
��HF=KF
��FΪMK�е�
���M������x��-![]() x2-
x2-![]() x+5��
x+5��
��F��0��2��
���K������-x��![]() x2+
x2+![]() x-1��
x-1��
��K���������y=![]() x1
x1
���x1=0��x2=-4��
��x=0����y=-![]() x2-
x2-![]() x+5�����y=5��
x+5�����y=5��
��x=-4����y=-![]() x2-
x2-![]() x+5
x+5
���y=3
���M������-4��3����0��5����

 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�