ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() СНЕу(Еу
СНЕу(Еу![]() дкЕу
дкЕу![]() ЕФзѓБп)гы
ЕФзѓБп)гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ,ХзЮяЯпЕФЖЅЕуЮЊ
,ХзЮяЯпЕФЖЅЕуЮЊ![]() .
.
(1)ЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
(2)Еу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕу(Еу
ЩЯвЛЕу(Еу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯ)ЃЌЙ§Еу
жиКЯ)ЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌгыжБЯп
жсЕФДЙЯпЃЌгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌгыХзЮяЯпНЛгкЕу
ЃЌгыХзЮяЯпНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛХзЮяЯпгкЕу
НЛХзЮяЯпгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ,ПЩЕУОиаЮ
,ПЩЕУОиаЮ![]() .ШчЭМЃЌЕу
.ШчЭМЃЌЕу![]() дкЕу
дкЕу![]() зѓБпЃЌЕБОиаЮ
зѓБпЃЌЕБОиаЮ![]() ЕФжмГЄзюДѓЪБЃЌЧѓДЫЪБЕФ
ЕФжмГЄзюДѓЪБЃЌЧѓДЫЪБЕФ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЕБОиаЮ![]() ЕФжмГЄзюДѓЪБЃЌСЌНг
ЕФжмГЄзюДѓЪБЃЌСЌНг![]() ЃЌЙ§ХзЮяЯпЩЯвЛЕу
ЃЌЙ§ХзЮяЯпЩЯвЛЕу![]() зї
зї![]() жсЕФЦНааЯпЃЌгыжБЯп
жсЕФЦНааЯпЃЌгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() (Еу
(Еу![]() дкЕу
дкЕу![]() ЕФЩЯЗН)Шє
ЕФЩЯЗН)Шє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.

ЁОД№АИЁП(1)![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ![]() ЃЛ(2)
ЃЛ(2)![]() ЃЛ(3)
ЃЛ(3)![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
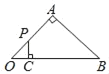
ЃЈ1ЃЉСю![]() ЃЌПЩЧѓГіAЁЂBСНЕузјБъЃЌСюx=0ЃЌПЩЧѓГіЕуCЕФзјБъЃЛЃЈ2ЃЉЧѓОиаЮЕФУцЛ§КЏЪ§НтЮіЪНЃЌЭЈЙ§ЖЅЕузјБъЧѓГіm,дйЧѓжБЯп
ЃЌПЩЧѓГіAЁЂBСНЕузјБъЃЌСюx=0ЃЌПЩЧѓГіЕуCЕФзјБъЃЛЃЈ2ЃЉЧѓОиаЮЕФУцЛ§КЏЪ§НтЮіЪНЃЌЭЈЙ§ЖЅЕузјБъЧѓГіm,дйЧѓжБЯп![]() ЕФНтЮіЪНЃЌЧѓГі
ЕФНтЮіЪНЃЌЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЛЃЈ3ЃЉжЄ
ЃЛЃЈ3ЃЉжЄ![]() гыдЕужиКЯЃЌ
гыдЕужиКЯЃЌ![]() Еугы
Еугы![]() ЕужиКЯЃЌЙЪ
ЕужиКЯЃЌЙЪ![]() ЃЌАб
ЃЌАб![]() ДњШы
ДњШы![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛЩш
ЃЛЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌЕУ
ЃЌЕУ![]() .НтЕУ
.НтЕУ![]() Лђ
Лђ![]() ЃЌПЩЕУFзјБъ.
ЃЌПЩЕУFзјБъ.
гЩХзЮяЯп![]() ПЩжЊЃЌ
ПЩжЊЃЌ![]() .
.
Сю![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
НтЕУЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
(2)гЩХзЮяЯп![]() ПЩжЊЃЌЖдГЦжсЮЊ
ПЩжЊЃЌЖдГЦжсЮЊ![]() .
.
![]() ЃЌPЃЈm,
ЃЌPЃЈm,![]() ЃЉ,N(-2-m,0)
ЃЉ,N(-2-m,0)
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ОиаЮ
ОиаЮ![]() ЕФжмГЄ
ЕФжмГЄ![]()
![]()
![]() ЃЌ
ЃЌ
![]() ОиаЮЕФжмГЄзюДѓЪБЃЌ
ОиаЮЕФжмГЄзюДѓЪБЃЌ![]() .
.
![]() ЃЌ
ЃЌ![]() ЩшжБЯп
ЩшжБЯп![]() ЕФНтЮіЪН
ЕФНтЮіЪН![]() ЃЌ
ЃЌ![]()
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() НтЮіЪН
НтЮіЪН![]() ЃЌСю
ЃЌСю![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() .
.
(3)![]() ЃЌХзЮяЯпЕФЖдГЦжсЮЊ
ЃЌХзЮяЯпЕФЖдГЦжсЮЊ![]() ЃЌ
ЃЌ
![]() гІгыдЕужиКЯЃЌ
гІгыдЕужиКЯЃЌ![]() Еугы
Еугы![]() ЕужиКЯЃЌ
ЕужиКЯЃЌ
![]() ЃЌАб
ЃЌАб![]() ДњШы
ДњШы![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() .
.
![]() ЃЌ
ЃЌ
![]()
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() Еу
Еу![]() дкЕу
дкЕу![]() ЕФЩЯЗНЧв
ЕФЩЯЗНЧв![]() ЃЌ
ЃЌ
![]() .НтЕУ
.НтЕУ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
![]() Лђ
Лђ![]() .
.