题目内容
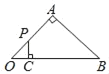
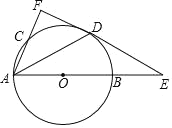
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,点D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
(1)求证:AF⊥EF.
(2)直接回答:
①已知AB=2,当BE为何值时,AC=CF?
②连接BD、CD、OC,当∠E等于多少度时,四边形OBDC是菱形?
【答案】(1)证明见解析;(2)①当BE=2时,AC=CF;②当∠E=30°时,四边形OBDC是菱形.
【解析】
(1)连接OD,由点D是弧BC的中点,过点D作⊙O的切线,可得OD⊥EF,AF∥OD,进而得出AF⊥EF;
(2)①当BE=2时,连接BC,证明△ACB∽△AFE,所以![]() ,即AC=CF;
,即AC=CF;
②当∠E=30°时,证明△ODB,△AOC,△COD为等边三角形,所以OB=BD=OD=CD=OC,即四边形OBDC是菱形.
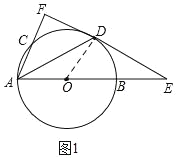
解:(1)如图1,连接OD,
∵点D是弧BC的中点,过点D作⊙O的切线,
∴OD⊥EF,∠CAD=∠DAB,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CAD=∠ADO,
∴AF∥OD,
∴AF⊥EF.
(2)①当BE=2时,AC=CF.
如图2,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AF⊥EF,
∴∠ACB=∠F=90°,
∴BC∥EF,
∴△ACB∽△AFE,
∴![]() ,
,
∴AC=CF.
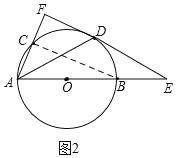
②当∠E=30°时,四边形OBDC是菱形.
如图3,∵过点D作⊙O的切线,
∴∠ODE=∠F=90°,
∴∠DOE=∠CAO=60°,
∵OD=OB=OC=OA,
∴△ODB,△AOC为等边三角形,
∴∠COA=∠DOB=60°,
∴∠COD=60°,
∴△COD为等边三角形,
∴OB=BD=OD=CD=OC,
∴四边形OBDC是菱形.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目