题目内容
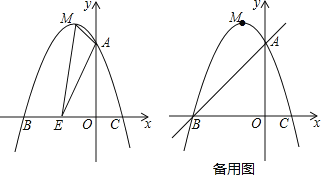
【题目】画出二次函数y=2x2+8x+6的图象.
(1)根据图象写出当y随x的增大而减小时x的范围;
(2)根据图象写出满足不等式2x2+8x+6<0的x的取值范围;
(3)求函数图象与两坐标轴交点所围成的三角形的面积.
【答案】(1)当x<-2时,y随x的增大而减小;(2)-3<x<1;(3)![]() .
.
【解析】
(1)先画出图象,再根据图象确定函数图象从左到右呈下降趋势的部分上点的横坐标的取值范围便可;
(2)根据函数图象在x轴下方部分的图象上点的横坐标的取值范围作答;
(3)根据函数图象与坐标轴的交点坐标求出三角形的底边与高,进而由三角形的面积公式求出面积.
列表
![]()
描点、连线
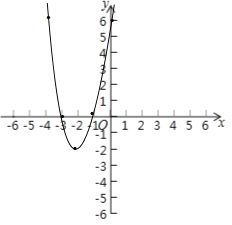
(1)由图象可知,当x<-2时,y随x的增大而减小;
(2)由图象可知,当-3<x<1时,函数图象在x轴下方,
∴不等式2x2+8x+6<0的x的取值范围为:-3<x<1;
(3)由图象可知,函数图象与两坐标轴交点所围成的三角形为△ABC,
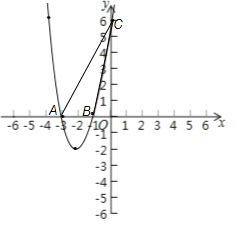
其A、B、C三点的坐标分别为:A(-3,0),B(-1,0),C(0,6),
∴AB=-1+3=2,OC=6,
∴![]() .
.

【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.