Question

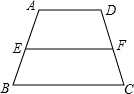
如图，梯形ABCD中，AD∥BC，∠D=90°，BC=CD=12，∠ABE=45°，点E在DC上，AE，BC的延长线相交于点F，若AE=10，则S_△ADE+S_△CEF的值是______．

Answer 1

如图，延长DA，过B作BM⊥DA，交其延长线于M．
∴四边形DCBM是正方形，
∴DM=BC=CD=12，再把△BEC旋转到△BMN的位置，
∴BN=BE，∠EBC=∠MBN，CE=MN
∵∠ABE=45°
∴∠EBC+∠ABM=90°-45°=45°
∴∠ABN=∠ABM+∠MBN=45°，AB公共
∴△ABN≌△ABE
∴AN=AE=10，设CE=x，那么MN=x，DE=CD-CE=12-x，AM=10-x，AD=12-AM=2+x，
在Rt△ADE中：AD²+DE²=AE²
∴（2+x）²+（12-x）²=10²
∴x₁=4，x₂=6，
当x=4时，CE=4，DE=8，AD=6
∵AD∥CF
∴△ADE∽△FCE，
∴

AD

CF

=

DE

CE

∴CF=3，
∴S_△ADE+S_△CEF=30；
当x=6时，CE=6，DE=6，AD=8
∵AD∥CF
∴△ADE∽△FCE
∴

AD

CF

=

DE

CE

∴CF=8
∴S_△ADE+S_△CEF=48．
综上所述，S_△ADE+S_△CEF的值是30或48．
故答案为：30或48．