题目内容
如图，梯形ABCD中，AD∥BC，AB=CD，AD=2，BC=6，∠B=60°，则梯形ABCD的周长是______．
过点A作AE⊥BC于点E，
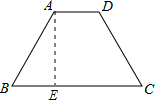∵ABCD是梯形，且AB=CD，
∴四边形ABCD是等腰梯形，
∴BE=
（BC-AD）=2，
在RT△ABE中，AB=
=4，
故可得梯形ABCD的周长=AD+AB+BC+DC=16．
故答案为：16．
∵ABCD是梯形，且AB=CD，∴四边形ABCD是等腰梯形，
∴BE=
| 1 |
| 2 |
在RT△ABE中，AB=
| BE |
| cos∠ABE |
故可得梯形ABCD的周长=AD+AB+BC+DC=16．
故答案为：16．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
