Question

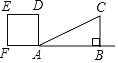
【题目】如图，在矩形中，，，点是边上的一个动点，将沿折叠，得到．连接、，若为等腰三角形，则的长为_______．

Answer 1

【答案】、、

【解析】

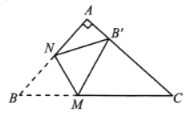
当的B′在矩形的内部时，分三种情形考虑：①DA＝DB′．②AD＝AB′．③B′A＝B′D．当点B′落在矩形的外部时，有一种情形DA＝DB′，分别求解即可．

解：如图，过点B′作MN⊥CD于M，交AB于N，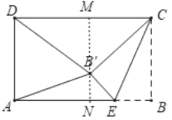

∵四边形ABCD是矩形，
∴AD＝BC＝13，CD＝AB＝24，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，
又∵MN⊥CD，
∴四边形ANMD是矩形，四边形BCMN是矩形，
∴AD＝MN＝13，AN＝DM，MC＝BN，
若AD＝DB′＝13，
∵将△CBE沿CE折叠，得到△CB′E连接AB′，
∴BC＝B′C＝13，BE＝B′E，
∴B′C＝B′D，
又∵MN⊥CD，
∴CM＝DM＝12，
∴B′M＝，

∴B′N＝13-5=8，
∵B′E2＝NE2＋B′N2，
∴BE2＝64＋（12BE）2，
∴BE＝；
∵AB′的最小值＝ACCB′＝，
AB′＞AD，
当B′A＝B′D时，

∵B′M＝B′N，
∴CB′＝2B′M，
∴∠B′CM＝30°，
∴∠ECB＝∠ECB′＝30°，
∴BE＝CBtan30°＝，
如图当点B′在直线CD的上方，AD＝DB′时，

同法可知DM＝CM＝12，MB′＝5，
在Rt△ENB′中，则有BE2＝（BE12）2＋182，
解得BE＝，
综上所述，满足条件的BE的值为或或，

故答案为：、、