ЬтФПФкШн
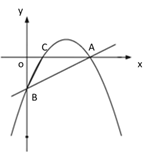
ЁОЬтФПЁПЁОЬтФПЁПШчЭМЂйЃЌвЛДЮКЏЪ§ yЃН![]() x - 2 ЕФЭМЯёНЛ x жсгкЕу AЃЌНЛ y жсгкЕу BЃЌЖўДЮКЏЪ§ yЃН
x - 2 ЕФЭМЯёНЛ x жсгкЕу AЃЌНЛ y жсгкЕу BЃЌЖўДЮКЏЪ§ yЃН![]() x2 bx cЕФЭМЯёОЙ§ AЁЂB СНЕуЃЌгы x жсНЛгкСэвЛЕу CЃЎ
x2 bx cЕФЭМЯёОЙ§ AЁЂB СНЕуЃЌгы x жсНЛгкСэвЛЕу CЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФЙиЯЕЪНМАЕу C ЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌШєЕу P ЪЧжБЯп AB ЩЯЗНЕФХзЮяЯпЩЯвЛЕуЃЌЙ§Еу P зї PDЁЮx жсНЛ AB гкЕу DЃЌPEЁЮy жсНЛ AB гкЕу EЃЌЧѓ PDЃЋPE ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌШєЕу M дкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЁЯAMBЃНЁЯACBЃЌЧѓГіЫљгаТњзуЬѕМўЕФЕу MЕФзјБъЃЎ
Ђй Ђк Ђл
ЁОД№АИЁП(1) yЃН![]() , CЃЈ1ЃЌ0ЃЉ;(2)6;(3) MЕФзјБъЮЊЃЈ
, CЃЈ1ЃЌ0ЃЉ;(2)6;(3) MЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ.
ЃЉ.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіAЁЂBЕФзјБъЃЌШЛКѓАбAЁЂBЕФзјБъЗжБ№ДњШыЖўДЮКЏЪ§ЕФНтЮіЪНЃЌНтЗНГЬзщМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЯШжЄУїЁїPDEЁзЁїOABЃЌЕУЕНPDЃН2PEЃЎЩшPЃЈmЃЌ ![]() ЃЉЃЌдђEЃЈmЃЌ
ЃЉЃЌдђEЃЈmЃЌ ![]() ЃЉЃЌPDЃЋPEЃН3PEЃЌШЛКѓХфЗНМДПЩЕУЕННсТлЃЎ
ЃЉЃЌPDЃЋPEЃН3PEЃЌШЛКѓХфЗНМДПЩЕУЕННсТлЃЎ
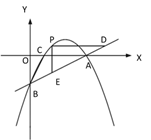
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃКЂйЕБЕуMдкдкжБЯпABЩЯЗНЪБЃЌдђЕуMдкЁїABCЕФЭтНгдВЩЯЃЌШчЭМ1ЃЎЧѓГідВаФO1ЕФзјБъКЭАыОЖЃЌРћгУMO1=АыОЖМДПЩЕУЕННсТлЃЎ
ЂкЕБЕуMдкдкжБЯпABЯТЗНЪБЃЌзїO1ЙигкABЕФЖдГЦЕуO2ЃЌШчЭМ2ЃЎЧѓГіЕуO2ЕФзјБъЃЌЫуГіDMЕФГЄЃЌМДПЩЕУЕННсТлЃЎ
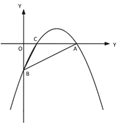
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉСюyЃН![]() ЃН0ЃЌЕУЃКxЃН4ЃЌЁрAЃЈ4ЃЌ0ЃЉЃЎ
ЃН0ЃЌЕУЃКxЃН4ЃЌЁрAЃЈ4ЃЌ0ЃЉЃЎ
СюxЃН0ЃЌЕУЃКyЃНЃ2ЃЌЁрBЃЈ0ЃЌЃ2ЃЉЃЎ
ЁпЖўДЮКЏЪ§yЃН![]() ЕФЭМЯёОЙ§AЁЂBСНЕуЃЌЁр
ЕФЭМЯёОЙ§AЁЂBСНЕуЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК 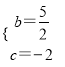 ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§ЕФЙиЯЕЪНЮЊyЃН![]() ЃЎ
ЃЎ
СюyЃН![]() ЃН0ЃЌНтЕУЃКxЃН1ЛђxЃН4ЃЌЁрCЃЈ1ЃЌ0ЃЉЃЎ
ЃН0ЃЌНтЕУЃКxЃН1ЛђxЃН4ЃЌЁрCЃЈ1ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЁпPDЁЮxжсЃЌPEЁЮyжсЃЌЁрЁЯPDEЃНЁЯOABЃЌЁЯPEDЃНЁЯOBAЃЌЁрЁїPDEЁзЁїOABЃЎЁр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН2ЃЌЁрPDЃН2PEЃЎЩшPЃЈmЃЌ
ЃН2ЃЌЁрPDЃН2PEЃЎЩшPЃЈmЃЌ ![]() ЃЉЃЌдђEЃЈmЃЌ
ЃЉЃЌдђEЃЈmЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЁрPDЃЋPEЃН3PEЃН3ЁС[(![]() )Ѓ(
)Ѓ(![]() )]ЃН
)]ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
Ёп0ЃМmЃМ4ЃЌЁрЕБmЃН2ЪБЃЌPDЃЋPEгазюДѓжЕ6ЃЎ
ЃЈ3ЃЉЂйЕБЕуMдкдкжБЯпABЩЯЗНЪБЃЌдђЕуMдкЁїABCЕФЭтНгдВЩЯЃЌШчЭМ1ЃЎ
ЁпЁїABCЕФЭтНгдВO1ЕФдВаФдкЖдГЦжсЩЯЃЌЩшдВаФO1ЕФзјБъЮЊЃЈ![]() ЃЌЃtЃЉЃЎ
ЃЌЃtЃЉЃЎ
Ёр![]() ЃН
ЃН![]() ЃЌНтЕУЃКtЃН2ЃЌЁрдВаФO1ЕФзјБъЮЊЃЈ
ЃЌНтЕУЃКtЃН2ЃЌЁрдВаФO1ЕФзјБъЮЊЃЈ![]() ЃЌЃ2ЃЉЃЌЁрАыОЖЮЊ
ЃЌЃ2ЃЉЃЌЁрАыОЖЮЊ![]() ЃЎ
ЃЎ
ЩшMЃЈ![]() ЃЌyЃЉЃЎЁпMO1=
ЃЌyЃЉЃЎЁпMO1=![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУЃКy=
ЃЌНтЕУЃКy=![]() ЃЌЁрЕуMЕФзјБъЮЊЃЈ
ЃЌЁрЕуMЕФзјБъЮЊЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЂкЕБЕуMдкдкжБЯпABЯТЗНЪБЃЌзїO1ЙигкABЕФЖдГЦЕуO2ЃЌШчЭМ2ЃЎ
ЁпAO1ЃНO1BЃН![]() ЃЌЁрЁЯO1ABЃНЁЯO1BAЃЎЁпO1BЁЮxжсЃЌЁрЁЯO1BAЃНЁЯOABЃЌЁрЁЯO1ABЃНЁЯOABЃЌO2дкxжсЩЯЃЌЁрЕуO2ЕФзјБъЮЊ ЃЈ
ЃЌЁрЁЯO1ABЃНЁЯO1BAЃЎЁпO1BЁЮxжсЃЌЁрЁЯO1BAЃНЁЯOABЃЌЁрЁЯO1ABЃНЁЯOABЃЌO2дкxжсЩЯЃЌЁрЕуO2ЕФзјБъЮЊ ЃЈ![]() ЃЌ0ЃЉЃЌЁрO2DЃН1ЃЌЁрDMЃН
ЃЌ0ЃЉЃЌЁрO2DЃН1ЃЌЁрDMЃН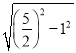 ЃН
ЃН![]() ЃЌЁрЕуMЕФзјБъЮЊЃЈ
ЃЌЁрЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃКЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПМЮаЫФГаЃзщжЏСЫЁАРЌЛјЗжРрЁБжЊЪЖОКШќЛюЖЏЃЌЛёНБЭЌбЇдкОКШќжаЕФГЩМЈЛцГЩШчЯТЭМБэЃЌ
ИљОнЭМБэЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
РЌЛјЗжРржЊЪЖОКШќЛюЖЏГЩМЈЭГМЦБэ
ЗжЪ§ЖЮ | ЦЕЪ§ | ЦЕЪ§ЦЕТЪ |
80ЁмxЃМ85 | x | 0.2 |
85ЁмxЃМ90 | 80 | y |
90ЁмxЃМ95 | 60 | 0.3 |
95ЁмxЃМ100 | 20 | 0.1 |
ЃЈ1ЃЉЧѓБОДЮЛёНБЭЌбЇЕФШЫЪ§ЃЛ
ЃЈ2ЃЉЧѓБэжаxЃЌyЕФЪ§жЕЃКВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЎ

ЁОЬтФПЁПФГСжГЁвЊПМВьвЛжжгзЪїдквЛЖЈЬѕМўЯТЕФвЦжВГЩЛюТЪЃЌдквЦжВЙ§ГЬжаЕФЭГМЦНсЙћШчЯТБэЫљЪОЃК
вЦжВЕФгзЪїn/ПУ | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
ГЩЛюЕФгзЪїm/ПУ | 423 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
ГЩЛюЕФЦЕТЪ | 0.846 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
дкДЫЬѕМўЯТЃЌЙРМЦИУжжгзЪївЦжВГЩЛюЕФИХТЪЮЊ_________________ЃЈОЋШЗЕН![]() ЃЉЃЛШєИУСжГЁгћЪЙГЩЛюЕФгзЪїДяЕН4.3ЭђПУЃЌдђЙРМЦашвЊвЦжВИУжжгзЪї_________ЭђПУ.
ЃЉЃЛШєИУСжГЁгћЪЙГЩЛюЕФгзЪїДяЕН4.3ЭђПУЃЌдђЙРМЦашвЊвЦжВИУжжгзЪї_________ЭђПУ.