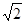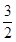题目内容
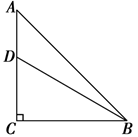
如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1: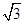 (指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,
(指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,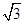 ≈1.732).
≈1.732).
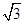 (指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,
(指坡面的铅直高度与水平宽度的比),且AB=20m.身高为1.7m的小明站在大堤A点,测得髙压电线杆顶端点D的仰角为30°.已知地面CB宽30m,求髙压电线杆CD的髙度(结果保留三个有效数字,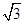 ≈1.732).
≈1.732).
髙压电线杆CD的髙度约39.0 m
试题分析:过点M作MN⊥DC,垂足为N,延长MA交CB延长线于点Q.

在Rt△AQB中,AB=20m,
∵i=
 =
= =
=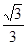 ,
,∴tan∠ABQ=
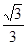 ,
,∴∠ABQ=30°. 1分
∴AQ=
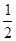 AB=10m,∴BQ=
AB=10m,∴BQ=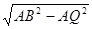 =
= m
m ∵MA=1.7m,∴MQ=" MA+" AQ=11.7m,∴NC=11.7m.
∵BC=30m,∴CQ=" BC+" BQ=30+
 (m),∴MN= CQ=30+
(m),∴MN= CQ=30+ (m).
(m). 在Rt△DNM中,∠DNM=90°,∠DMN=30°,
∴
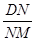 = tan30°=
= tan30°=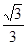 ,∴DN=MN×
,∴DN=MN×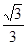 =
=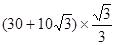 =
= ,
, ∴DC=" DN+" NC=
 +11.7≈10×1.732+10+11.7≈39.0(m).
+11.7≈10×1.732+10+11.7≈39.0(m). 答:髙压电线杆CD的髙度约39.0 m.
点评:本题考查三角函数,平行线,要求考生掌握平行线的性质,熟悉三角函数的定义,会利用定义解答本题

练习册系列答案
相关题目
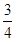
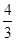
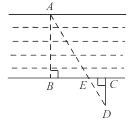
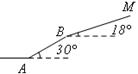
 ,则AD的长为( )
,则AD的长为( )