题目内容
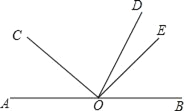
【题目】如图，O为直线AB上一点，∠AOC=52°，OD平分∠AOC，OD⊥OE，垂足为点O．
（1）求∠BOD的度数；
（2）说明OE平分∠BOC．
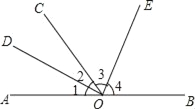
【答案】（1）154°；（2）OE平分∠BOC．理由见解析.
【解析】
（1）根据角平分线的定义得到∠1的度数，再利用邻补角的定义即可得到结论；
（2）分别求得∠3与∠4的度数即可说明．
（1）∵∠AOC=52°，OD平分∠AOC，∴∠1==∠2=
∠AOC=26°，∴∠BOD=180°－∠1=154°；
（2）OE平分∠BOC．理由如下：
∵OD⊥OE，∴∠DOE=90°．
∵∠DOC=26°，∴∠3=∠DOE﹣∠2=90°﹣26°=64°．
又∵∠4=∠BOD﹣∠DOE=154°﹣90°=64°，∴∠3=∠4，∴OE平分∠BOC．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
相关题目
