题目内容
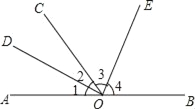
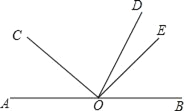
【题目】如图，点O是直线AB上一点，OD平分∠BOC，∠COE=90°.
（1）若∠AOC=48°，求∠DOE的度数．
（2）若∠AOC=α，则∠DOE= （用含α的代数式表示）．
【答案】(1) ∠DOE=24°；(2)
α．
【解析】
（1）先由邻补角定义求出∠BOC=180°-∠AOC=132°，再根据角平分线定义得到∠COD=∠BOC=66°，那么∠DOE=∠COE-∠COD=24°；
（2）先由邻补角定义求出∠BOC=180°-∠AOC=180°-α，再根据角平分线定义得到∠COD=∠BOC，于是得到结论．
解：（1）∵O是直线AB上一点，
∴∠AOC+∠BOC=180°，
∵∠AOC=48°，
∴∠BOC=132°，
∵OD平分∠BOC，
∴∠COD=
∠BOC=66°，
∵∠DOE=∠COE﹣∠COD，∠COE=90°，
∴∠DOE=90°﹣66°=24°；
（2）∵O是直线AB上一点，
∴∠AOC+∠BOC=180°，
∵∠AOC=α，
∴∠BOC=180°﹣α，
∵OD平分∠BOC，
∴∠COD=
∠BOC=（180°﹣α）=90°﹣α，
∵∠DOE=∠COE﹣∠COD，∠COE=90°，
∴∠DOE=90°﹣（90°﹣α）=α．
故答案为：α．
【题目】寒假结束了，为了了解九年级学生寒假体育锻炼情况，王老师调查了九年级所有学生寒假体育锻炼时间，并随即抽取10名学生进行统计，制作出如下统计图表：
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题：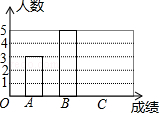
（1）将条形统计图补充完整；
（2）若用扇形统计图来描述10名学生寒假体育锻炼情况，分别求A，B，C三个等级对应的扇形圆心角的度数；
（3）已知这次统计中共有60名学生寒假体育锻炼时间是A等，请你估计这次统计中B等，C等的学生各有多少名？
