题目内容
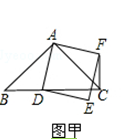
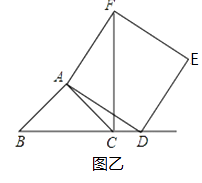
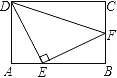
【题目】如图1,线段AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
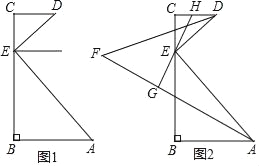
(2)如图2,AF、DF分别平分∠BAE和∠CDE,EH平分∠DEC交CD于点H,EH的反向延长线交AF于点G.
①求证EG⊥AF;
②求∠F的度数.(提示:三角形内角和等于180度)
【答案】(1)证明见解析;(2)①证明见解析;②45°.
【解析】
(1)利用同角的余角相等即可证明;
(2)①想办法证明∠EAG+∠AEG=90°即可解决问题;
②利用∠DFA=∠DFM+∠AFM=![]() ∠CDE+
∠CDE+![]() ∠EAB=
∠EAB=![]() (∠CDE+∠EAB)即可解决问题.
(∠CDE+∠EAB)即可解决问题.
(1)∵AB⊥BC,
∴∠EAB+∠AEB=90°,
∵AE⊥ED,
∴∠CED+∠AEB=90°,
∴∠EAB=∠CED.
(2)①∵AF平分∠BAE,
∴∠EAG=![]() ∠EAB,
∠EAB,
∵EH平分∠BAE,
∴∠HED=![]() ∠CED,
∠CED,
∵∠EAB=∠CED,
∴∠HED=∠EAG,
∴∠HED+∠AEG=90°,
∴∠EAG+∠AEG=90°,
∴∠EGA=90°,
∴EG⊥AF.
②作FM∥CD,
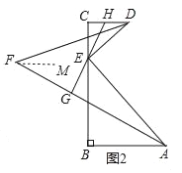
∵AB⊥BC,CD⊥BC,
∴AB∥CD,
∴FM∥AB,
∴∠DFM=∠CDF=![]() ∠CDE,∠AFM=∠FAB=
∠CDE,∠AFM=∠FAB=![]() ∠EAB,
∠EAB,
∵∠CDE+∠CED=90°,
∴∠CDE+∠EAB=90°,
∴∠DFA=∠DFM+∠AFM=![]() ∠CDE+
∠CDE+![]() ∠EAB=
∠EAB=![]() (∠CDE+∠EAB)=45°.
(∠CDE+∠EAB)=45°.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目