题目内容
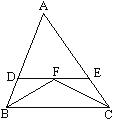
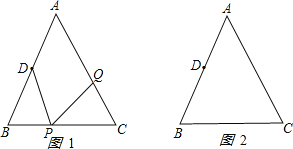
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
【答案】(1)全等,理由见解析;(2)![]() cm/s
cm/s
【解析】
试题(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.
(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等,则可知PB=3tcm,PC=8﹣3tcm,CQ=xtcm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.
解:(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,
∵△ABC中,AB=AC,
∴在△BPD和△CQP中,
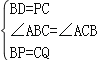 ,
,
∴△BPD≌△CQP(SAS).
(2)设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等;则可知PB=3tcm,PC=8﹣3tcm,CQ=xtcm,
∵AB=AC,
∴∠B=∠C,
根据全等三角形的判定定理SAS可知,有两种情况:①当BD=PC,BP=CQ时,②当BD=CQ,BP=PC时,两三角形全等;
①当BD=PC且BP=CQ时,8﹣3t=5且3t=xt,解得x=3,∵x≠3,∴舍去此情况;
②BD=CQ,BP=PC时,5=xt且3t=8﹣3t,解得:x=![]() ;
;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为![]() cm/s时,能够使△BPD与△CQP全等.
cm/s时,能够使△BPD与△CQP全等.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题: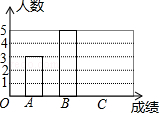
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?