题目内容
【题目】设函数y=x2+2kx+k﹣1(k为常数),下列说法正确的个数是( )
(1)对任意实数k,函数与x轴有两个交点
(2)当x≥﹣k时,函数y的值都随x的增大而增大
(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上
(4)对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点
A.1B.2C.3D.4
【答案】D
【解析】
(1)△=b2﹣4ac=4k2﹣4k+4=(2k﹣1)2+3>0,即可求解;
(2)函数的对称轴为:x=﹣![]() =﹣k,a>0,即可求解;
=﹣k,a>0,即可求解;
(3)函数的对称轴为:x=﹣k,则顶点坐标为:(﹣k,﹣k2+k﹣1),即可求解;
(4)y=x2+2kx+k﹣1=x2+k(2x+1)﹣1,当x=﹣![]() 时,y=﹣
时,y=﹣![]() ,即可求解.
,即可求解.
(1)△=b2﹣4ac=4k2﹣4k+4=(2k﹣1)2+3>0,故对任意实数k,函数与x轴有两个交点,符合题意;
(2)函数的对称轴为:x=﹣![]() =﹣k,a>0,故当x≥﹣k时,函数y的值都随x的增大而增大,符合题意;
=﹣k,a>0,故当x≥﹣k时,函数y的值都随x的增大而增大,符合题意;
(3)函数的对称轴为:x=﹣k,则顶点坐标为:(﹣k,﹣k2+k﹣1),故顶点在抛物线:y=﹣x2﹣x﹣1上,k取不同的值时,二次函数y的顶点始终在同一条抛物线上,符合题意;
(4)y=x2+2kx+k﹣1=x2+k(2x+1)﹣1,当x=﹣![]() 时,y=﹣
时,y=﹣![]() ,故对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点,符合题意;
,故对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点,符合题意;
故选:D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
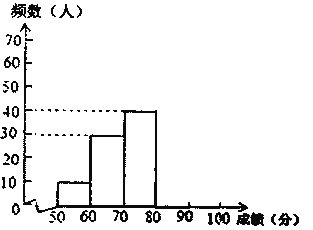
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?