题目内容
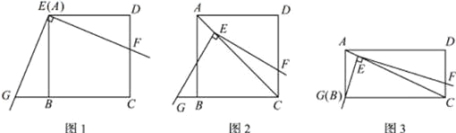
【题目】如图1.正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
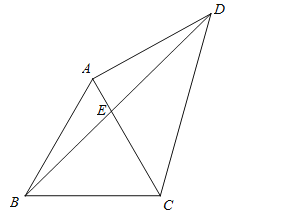
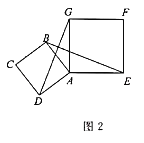
![]() 如图2.将线段
如图2.将线段![]() 绕点
绕点![]() 逆时针旋转,设旋转角为
逆时针旋转,设旋转角为![]() ,并以
,并以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() 试问随着线段
试问随着线段![]() 的旋转,
的旋转,![]() 与
与![]() 有怎样的数量关系?说明理由;
有怎样的数量关系?说明理由;
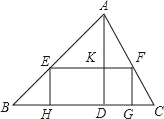
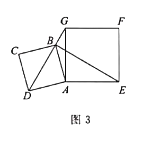
![]() 如图3,在
如图3,在![]() 的条件下,若点
的条件下,若点![]() 恰好落在线段
恰好落在线段![]() 上,求点
上,求点![]() 走过的路径长(保留
走过的路径长(保留![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用已知条件得出![]() ,从而可得出结论
,从而可得出结论
(2) 连接![]() ,交
,交![]() 于
于![]() 连接
连接![]() ,可得出CG=AG,接着可证明
,可得出CG=AG,接着可证明![]() 是等边三角形.,再找出
是等边三角形.,再找出![]() ,最后利用弧长公式求解即可.
,最后利用弧长公式求解即可.
解:![]()
![]() .
.
理由如下:
由题意,可知![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
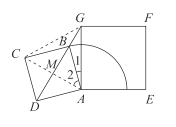
![]() 如图,连接
如图,连接![]() ,交
,交![]() 于
于![]() 连接
连接![]() .
.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() 与
与![]() 互相垂直平分.
互相垂直平分.
![]() 点
点![]() 在线段
在线段![]() 上,
上,
![]() 垂直平分
垂直平分![]() .
.
![]() .
.
由题意,知![]() ,
,
![]() .
.
又正方形![]() 的边长为
的边长为![]() ,
,
![]() .
.
![]() ,即
,即![]() 是等边三角形.
是等边三角形.
![]()
![]() .
.
![]() .
.
则点![]() 走过的路径长就是以
走过的路径长就是以![]() 为圆心,
为圆心,![]() 长为半径,且圆心角为105°的一段弧的弧长.
长为半径,且圆心角为105°的一段弧的弧长.
即![]()
所以点![]() 走过的路径长是
走过的路径长是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,其中相应等级的得分依次为
四个等级,其中相应等级的得分依次为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图:
分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图:
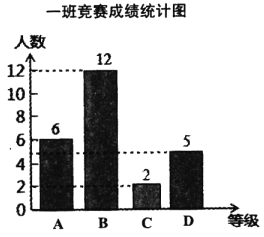
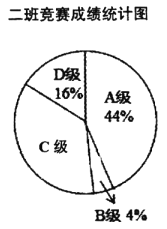
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在![]() 分及其以上的人数是_______人;
分及其以上的人数是_______人;
(2)补全下表中![]() 、
、![]() 、
、![]() 的值:
的值:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
一班 |
|
|
|
|
二班 |
|
|
|
|
(3)学校准备在这两个班中选一个班参加市级科学素养竞赛,你建议学校选哪个班参加?说说你的理由.