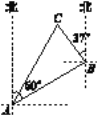题目内容
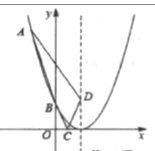
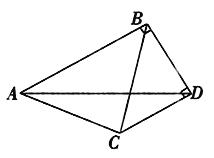
【题目】如图,△ABD和△BDC都是直角三角形,且∠ABD=∠BDC=90°,∠BAD=30°,∠DBC=45°,则tan∠DAC的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
过点C作CE⊥AD于点E,设BD=1,根据30°锐角所对的的直角边等于斜边的一半,和等腰直角三角形的性质,得CE=![]() CD=
CD=![]() ,ED=CD×cos∠CDE=
,ED=CD×cos∠CDE=![]() ,再得出AE的长,因为Rt△AEC中,tan∠DAC=
,再得出AE的长,因为Rt△AEC中,tan∠DAC=![]() ,即可解答.
,即可解答.
解:如图,过点C作CE⊥AD于点E,
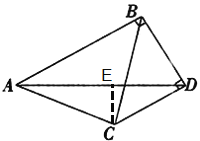
∵∠ABD=∠BDC=90°,∠BAD=30°,∠DBC=45°,设BD=1,
∴DC=BD=1,AD=2BD=2,AB∥CD
∴∠BAD=∠CDE=30°
∴CE=![]() CD=
CD=![]() , ED=CD×cos∠CDE=
, ED=CD×cos∠CDE=![]()
∴AE=AD-ED=2-![]()
在Rt△AEC中,tan∠DAC=![]() =
=![]() =
= ![]() .
.
故选:C.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目