题目内容
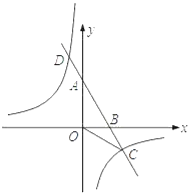
【题目】如图,二次函数![]() 的图像经过点
的图像经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 、
、![]() 分别为
分别为![]() 轴、直线
轴、直线![]() 上的动点,当四边形
上的动点,当四边形![]() 的周长最小时,
的周长最小时,![]() 所在直线对应的函数表达式是( )
所在直线对应的函数表达式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
利用对称性和两点之间线段最短,作出辅助线,将A代入求出函数解析式,进而求出G(3,4),B(0,1),H(0,-1),待定系数法即可求出直线解析式.
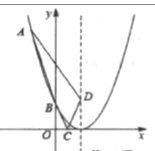
解:如下图,取A关于抛物线的对称轴的对应点G,B关于x轴的对称点H,连接HG,与抛物线的对称轴交于点D,与x轴的交点为点C,连接AD,CD,BC,
利用对称的性质可知DA=DG,CB=CH,
∵两点之间线段最短,并且此时H,C,D,G四点共线,
∴此时的四边形ABCD是周长最小的,
将![]() 代入
代入![]() 中得,a=1,
中得,a=1,
∴抛物线的解析式为![]() ,
,
∴抛物线的对称轴为直线x=1,
∴G(3,4),B(0,1),H(0,-1)
设直线CD的解析式为y=kx+b,(k![]() 0)
0)
代入G(3,4), H(0,-1)得
![]()
解得: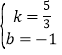 ,
,
∴直线CD的解析式为![]()
故选D.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目