Question

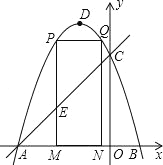
【题目】如图，抛物线 y＝﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点（点 A 在点 B 的左边），与 y轴交于点 C，点 D 为抛物线的顶点．

（1）求点 A、B、C 的坐标；

（2）点 M（m，0）为线段 AB 上一点（点 M 不与点 A、B 重合），过点 M 作 x 轴的垂线，与直线 AC 交于点 E，与抛物线交于点 P，过点 P 作 PQ∥AB 交抛物线于点 Q，过点 Q 作 QN⊥x 轴于点 N，可得矩形 PQNM．如图，点 P 在点 Q 左边，试用含 m 的式子表示矩形 PQNM 的周长；

（3）当矩形 PQNM 的周长最大时，m 的值是多少？并求出此时的△AEM 的面积；

（4）在（3）的条件下，当矩形 PMNQ 的周长最大时，连接 DQ，过抛物线上一点 F 作 y 轴的平行线，与直线 AC 交于点 G（点 G 在点 F 的上方）．若 FG＝2DQ，求点 F 的坐标．

Answer 1

【答案】（1）A（﹣3，0），B（1，0）；（2）矩形 PMNQ 的周长＝﹣2m2﹣8m+2；（3）矩形的周长最大时，m＝﹣2；△AEM的面积为 ；（4）F（﹣4，﹣5）或（1，0）．

【解析】

（1）利用函数图象与坐标轴的交点的求法，求出点A，B，C的坐标；

（2）先确定出抛物线对称轴，用m表示出PM，MN即可；

（3）由（2）得到的结论判断出矩形周长最大时，确定出m，进而求出直线AC的解析式即可；

（4）在（3）的基础上，判断出N应与原点重合，Q点与C点重合，求出DQ＝DC＝2，再建立方程（n+3）﹣（﹣n2﹣2n+3）＝4即可．

（1）由抛物线 y＝﹣x2﹣2x+3 可知，C（0，3）．令 y＝0，则 0＝﹣x2﹣2x+3，

解得，x＝﹣3 或 x＝l，

∴A（﹣3，0），B（1，0）．

（2）由抛物线 y＝﹣x2﹣2x+3 可知，对称轴为 x＝﹣1．

∵M（m，0），

∴PM＝﹣m2﹣2m+3，MN＝（﹣m﹣1）×2＝﹣2m﹣2，

∴矩形 PMNQ 的周长＝2（PM+MN）＝（﹣m2﹣2m+3﹣2m﹣2）×2＝﹣2m2﹣8m+2．

（3）∵﹣2m2﹣8m+2＝﹣2（m+2）2+10，

∴矩形的周长最大时，m＝﹣2．

∵A（﹣3，0），C（0，3）， 设直线 AC 的解析式 y＝kx+b，

∴

解得 k＝l，b＝3，

∴解析式 y＝x+3， 令 x＝﹣2，则 y＝1，

∴E（﹣2，1），

∴EM＝1，AM＝1，

∴S＝AM×EM＝，

即△AEM的面积为.

（4）∵M（﹣2，0），抛物线的对称轴为 x＝﹣l，

∴N 应与原点重合，Q 点与 C 点重合，

∴DQ＝DC，

把 x＝﹣1 代入 y＝﹣x2﹣2x+3，解得 y＝4，

∴D（﹣1，4），

∴DQ＝DC＝．

∵FG＝DQ，

∴FG＝4．

设 F（n，﹣n2﹣2n+3），则 G（n，n+3），

∵点 G 在点 F 的上方且 FG＝4，

∴（n+3）﹣（﹣n2﹣2n+3）＝4． 解得 n＝﹣4 或 n＝1，

∴F（﹣4，﹣5）或（1，0）．