题目内容
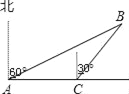
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
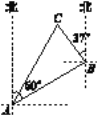
【答案】救援船的航行速度大约是64海里/时.
【解析】试题解析:辅助线如图所示:BD⊥AD,BE⊥CE,CF⊥AF,在Rt△ABD中,根据勾股定理可求AD,在Rt△BCE中,根据三角函数可求CE,EB,在Rt△AFC中,根据勾股定理可求AC,再根据路程÷时间=速度求解即可.
试题解析:解:辅助线如图所示:
BD⊥AD,BE⊥CE,CF⊥AF,有题意知,∠FAB=60°,∠CBE=37°,∴∠BAD=30°,∵AB=20海里,∴BD=10海里,在Rt△ABD中,AD=![]() =
=![]() ≈17.32海里,在Rt△BCE中,sin37°=
≈17.32海里,在Rt△BCE中,sin37°=![]() ,∴CE=BCsin37°≈0.6×10=6海里,∵cos37°=
,∴CE=BCsin37°≈0.6×10=6海里,∵cos37°=![]() ,∴EB=BCcos37°≈0.8×10=8海里,EF=AD=17.32海里,∴FC=EF﹣CE=11.32海里,AF=ED=EB+BD=18海里,在Rt△AFC中,AC=
,∴EB=BCcos37°≈0.8×10=8海里,EF=AD=17.32海里,∴FC=EF﹣CE=11.32海里,AF=ED=EB+BD=18海里,在Rt△AFC中,AC=![]() =
=![]() ≈21.26海里,21.26×3≈64海里/小时.
≈21.26海里,21.26×3≈64海里/小时.
答:救援的艇的航行速度大约是64海里/小时.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目