Question

【题目】下列命题中，正确的是( )

A. 两个相似三角形面积比为2：3，则周长比是4：9

B. 相似图形一定构成位似图形

C. 如果点D、E分别在△ABC的边AB、AC上，△ABC与△ADE相似，则DE∥BC

D. 在Rt△ABC中，斜边上的高CD2＝ADBD

Answer 1

【答案】D

【解析】

两个相似三角形面积比为2：3，则周长比是：；

相似图形不一定构成位似图形，但位似图形是相似图形；
如果点D、E分别在△ABC的边AB、AC上，△ABC与△ADE相似，则可能DE∥BC或AD：AC=AE：AB，即将图形反转相似；
在Rt△ABC中，斜边上的高CD2=ADBD．所以正确的是D．

解：A、两个相似三角形面积比为2：3，则周长比是：；

B、相似图形不一定构成位似图形，但位似图形是相似图形；

C、如果点D、E分别在△ABC的边AB、AC上，△ABC与△ADE相似，则可能DE∥BC或AD：AC＝AE：AB，即将图形反转相似；

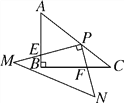
D、如图：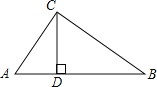

∵CD⊥AB，∠ACB＝90°

∴∠ADC＝∠BDC＝90°

∴∠A+∠ACD＝90°，∠A+∠B＝90°

∴∠ACD＝∠B

∴△ACD∽△CBD

∴AD：CD＝CD：BD

∴CD2＝ADBD

故选：D．