Question

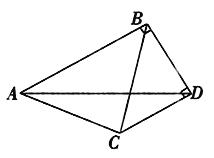
【题目】如图，四边形ABCD中，AD∥BC，AB=DC，AD=3cm，BC=7cm，∠B=60°，P为BC边上一点（不与B，C重合），连接AP，过P点作PE交DC于E，使得∠APE=∠B．

（1）求证：△ABP∽△PCE；

（2）求AB的长；

（3）在边BC上是否存在一点P，使得DE：EC=5：3？如果存在，求BP的长；如果不存在，请说明理由．

Answer 1

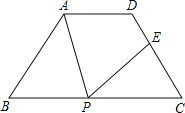
【答案】（1）见解析。（2）4.（3）见解析。BP=1或BP=6

【解析】

（1）先利用平角的定义和三角形的内角和定理判断出∠BAP=∠CPE，再判断出四边形ABCD是等腰梯形，进而得出∠B=∠C，即可得出结论；

（2）利用等腰梯形的性质求出BF，进而求出AB，即可得出结论；

（3）先求出CD=4，进而求出CE，最后借助（1）的结论得出比例式建立方程求解，即可得出结论．

解：（1）在△ABP中，∠B+∠BAP+∠APB=180°

∵∠APE=∠B，

∴∠APE+∠BAP+∠APB=180°，

∵∠APB+∠APE+∠CPE=180°，

∴∠BAP=∠CPE，

∵AD∥BC，AD=3，BC=7，

∴四边形ABCD是梯形，

∵AB=DC，

∴∠B=∠C，

∴△ABP∽△PCE；

（2）如图，

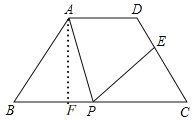
过点A作AF⊥BC于F，

在梯形ABCD中，AB=CD，

∴BF=（BC-AD）=2，

在Rt△ABF中，∠B=60°，

∴∠BAF=30°，

∴AB=2BF=4；

（3）由（2）知，AB=4，

∵CD=AB，

∴CD=4，

∵DE：EC=5：3，

∴CE=CD=×4=，

∵BC=7，

∴CP=BC-BP=7-BP，

由（1）知，△ABP∽△PCE，

∴，∴=，

∴BP2-7BP+6=0，

∴BP=1或BP=6，

∵点P在BC上，

∴0＜BP＜7，

∴BP=1或BP=6．