题目内容
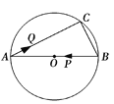
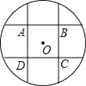
【题目】如图,边长为2的正方形ABCD各边的延长线和反向延长线与⊙O的交点把⊙O分成8条相等的弧,则⊙O的半径是_____.
【答案】![]()
【解析】
连接MN,EW,MW,QM,证四边形QMNW和BWNC是矩形,推出WN=QM=EW=2,根据勾股定理求出BE=BW=![]() ,在Rt△MQW中根据勾股定理求出半径即可.
,在Rt△MQW中根据勾股定理求出半径即可.
解:连接MN,EW,MW,QM,
∵弧QM=弧WN,
∴QM∥WN,QM=WN,∠WNM=![]() ×360°×4×
×360°×4×![]() =90°,
=90°,
∴四边形QMNW是矩形,
∴O在MW上,
∵正方形ABCD,
∴∠WBC=∠BCN=90°,
∴四边形BCNW是矩形,
∴WN=QM=EW=2,
∵∠BEW=∠EWB=45°,
∴由勾股定理得:EB=BW=![]() ,
,
同理AQ=![]() ,
,
设圆O的半径是r,
在Rt△MQW中,由勾股定理得:MQ2+QW2=MW2,
∴22+(![]() )2=(2r)2
)2=(2r)2
r=![]() ,
,
故答案为: ![]() .
.

练习册系列答案
相关题目
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0