题目内容
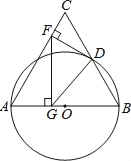
【题目】如图,在矩形ABCD中,AB=8,AD=12,过点A,D两点的⊙O与BC边相切于点E,求⊙O的半径.

【答案】⊙O的半径为6.25.
【解析】
首先连接OE,并反向延长交AD于点F,连接OA,由在矩形ABCD中,过A,D两点的⊙O与BC边相切于点E,易得四边形CDFE是矩形,由垂径定理可求得AF的长,然后设⊙O的半径为x,则OE=EF-OE=8-x,利用勾股定理即可得:(8-x)2+36=x2,继而求得答案.
连接OE,并反向延长交AD于点F,连接OA,
∵BC是切线,∴OE⊥BC,∴∠OEC=90°,
∵四边形ABCD是矩形,∴∠C=∠D=90°,∴四边形CDFE是矩形,
∴EF=CD=AB=8,OF⊥AD,∴AF=![]() AD=
AD=![]() ×12=6,
×12=6,
设⊙O的半径为x,则OE=EF﹣OE=8﹣x,
在Rt△OAF中,OF2+AF2=OA2,则(8﹣x)2+36=x2,
解得:x=6.25,∴⊙O的半径为:6.25.

练习册系列答案
相关题目