题目内容
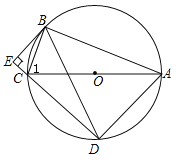
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线.
(2)若CD=2![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.

【答案】(1)证明见解析;(2)BF=![]() .
.
【解析】
(1)欲证明直线BF是⊙O的切线,只要证明AB⊥BF即可.
(2)连接OD,在Rt△ODE中,利用勾股定理求出由△APD∽△ABF,![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
(1)∵∠AFB=∠ABC,∠ABC=∠ADC,∴∠AFB=∠ADC,
∴CD∥BF,∴∠AFD=∠ABF,
∵CD⊥AB,∴AB⊥BF,∴直线BF是⊙O的切线.
(2)连接OD,∵CD⊥AB,∴PD=0.5CD=![]() ,
,
∵OP=1,∴OD=2,∵∠PAD=∠BAF,∠APO=∠ABF,∴△APD∽△ABF,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴BF=
,∴BF=![]() .
.

 名师金手指领衔课时系列答案
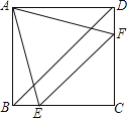
名师金手指领衔课时系列答案【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
;③BE+DF=EF;④∠AEB=75°.其中正确的序号是______.
【题目】争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分):78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93,整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) | 频数 |
| 5 |
|
|
| 11 |
|
|
| 2 |
回答下列问题:
(1)以上30个数据中,中位数是_____;频数分布表中![]() ____;
____;![]() _____;
_____;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.